[R] 적합도 검정
반응형
## [1] "ko_KR.UTF-8"1. Chi-square test
- 대부분의 통계적 모형에서는 종종 데이터가 특정 분포를 따름을 가정으로 합니다.
- 특히 데이터의 크기가 충분히 많다면 데이터가 정규 분포를 따름을 별 의심 없이 가정하기도 합니다.
- 하지만 실제로 그 분포를 따르는지 확인해볼 필요도 있습니다.
- 이와 관련하여 여러 방법이 존재하지만 이 때도 독립성 검정과 마찬가지로 분할표를 작성한 후 카이제곱검정을 사용할 수 있습니다.
- 이전 포스팅에서 했던 방식과 동일하게 예제를 통해 설명드리겠습니다.
- 데이터는
MASS라이브러리에 내장되어 있는survey데이터를 사용합니다.
library(MASS)
data(survey)survey는 학생 설문 조사 데이터입니다.str()함수를 이요해서 데이터의 구조를 살펴보겠습니다.
str(survey)## 'data.frame': 237 obs. of 12 variables:
## $ Sex : Factor w/ 2 levels "Female","Male": 1 2 2 2 2 1 2 1 2 2 ...
## $ Wr.Hnd: num 18.5 19.5 18 18.8 20 18 17.7 17 20 18.5 ...
## $ NW.Hnd: num 18 20.5 13.3 18.9 20 17.7 17.7 17.3 19.5 18.5 ...
## $ W.Hnd : Factor w/ 2 levels "Left","Right": 2 1 2 2 2 2 2 2 2 2 ...
## $ Fold : Factor w/ 3 levels "L on R","Neither",..: 3 3 1 3 2 1 1 3 3 3 ...
## $ Pulse : int 92 104 87 NA 35 64 83 74 72 90 ...
## $ Clap : Factor w/ 3 levels "Left","Neither",..: 1 1 2 2 3 3 3 3 3 3 ...
## $ Exer : Factor w/ 3 levels "Freq","None",..: 3 2 2 2 3 3 1 1 3 3 ...
## $ Smoke : Factor w/ 4 levels "Heavy","Never",..: 2 4 3 2 2 2 2 2 2 2 ...
## $ Height: num 173 178 NA 160 165 ...
## $ M.I : Factor w/ 2 levels "Imperial","Metric": 2 1 NA 2 2 1 1 2 2 2 ...
## $ Age : num 18.2 17.6 16.9 20.3 23.7 ...- 우리가 여기서 살펴볼 부분은 아래 두 변수입니다.
- W.Hnd: 왼손잡이인지 오른손잡이 인지를 나타내는 팩터형 변수
- 해당 변수를 가지고 왼손잡이와 오른손잡이의 비율이 30%:70% 인지 해당 여부를 확인해보겠습니다.
- 먼저 분할표를 작성합니다.
xtabs()함수를 이용합니다.
x <- xtabs(~ W.Hnd, data = survey)
x## W.Hnd
## Left Right
## 18 218- 실제로는 약 8%:92% 비율로 구성되어 있긴 합니다.
- 이제
chisq.test()함수를 통하여 카이제곱 검정을 수행할 수 있습니다.parguments를 이용하여 가설에 맞는 비율을 설정할 수 있습니다.
chisq.test(x, p = c(0.3, 0.7))##
## Chi-squared test for given probabilities
##
## data: x
## X-squared = 56.252, df = 1, p-value = 6.376e-14- 그 결과 p-value는 0.05 보다 훨씬 작으므로 유의수준 0.05 하에 왼손잡이와 오른손잡이 비율은 3:7 이라는 귀무가설을 기각할 수 있습니다.
2. Shapiro-Wilk test
- 샤피로 윌크 검정(Shapiro-Wilk test)은 표본이 정규분포로부터 추출된 것인지를 확인하기 위한 검정방법입니다.
shapiro.test()함수를 사용하며 이 때 귀무가설은 주어진 표본이 정규분포를 따른다는 것 입니다.- rnorm() 함수를 사용하여 표준정규분포를 따르는 랜덤샘플 1000개를 생성한 후 샤피로 윌크 검정을 수행한 결과는 다음과 같습니다.
x <- rnorm(n = 1000, mean = 0, sd = 1)
shapiro.test(x)##
## Shapiro-Wilk normality test
##
## data: x
## W = 0.99803, p-value = 0.2937- 그 결과 p-value는 0.05 보다 작으므로 유의수준 0.05 하에 귀무가설을 기각할 수 없습니다. 즉 정규분포를 따른다고 볼 수 있습니다.
3. Kolmogorov-Smirnov test
- 콜모고로프 스미르노프 검정(Kolmogorov-Smirnov test)은 데이터의 누적분포함수와 비교하고자 하는 분포의 누적분포함수 간의 최대 거리를 통계량으로 사용하는 가설검정 방법입니다.
ks.test()함수를 이용하여 검정을 시행할 수 있습니다.- x, y: 숫자 벡터 또는 누적분포함수
- alternative: 대립가설을 설정하는 argument로 양측검정일 경우는 alternative = “two.sided”
ks.test(x, y, alternative = c("two.sided", "less", "greater"))x <- rnorm(n = 100, mean = 0, sd = 1)
y <- rnorm(n = 100, mean = 2, sd = 1)
ks.test(x, y)##
## Two-sample Kolmogorov-Smirnov test
##
## data: x and y
## D = 0.74, p-value < 2.2e-16
## alternative hypothesis: two-sided- 분산은 같고 평균이 서로 다른 정규분포로부터 랜덤샘플을 발생하여 두 객체 간의 검정을 시행한 결과 p-value는 0.05보다 작으므로 유의수준 0.05 하에 귀무가설을 기각합니다.
- 즉, 두 객체는 서로 같은 분포로부터 나왔다고 볼 수 없습니다.
4. Q-Q plot
- Q-Q plot은 데이터가 특정 분포를 따르는지 시각적으로 검토하는 방법 중 하나입니다.
- 여기서 Q는 분위수(Quantile)의 약어로 Q-Q plot이 의미하는 바는 비교하고자 하는 분포의 분위수끼리 좌표평면에 표시하여 그린 그림이라고 생각할 수 있습니다.
- 분위수들을 plot에 표시하고 나면 데이터의 분위수와 비교하고자 하는 분포의 분위수 간에 직선 관계가 보이는지 확인할 수 있습니다.
- 예를 들어 임의의 확률변수 \(X\)가 정규분포를 따르는지 살펴보고 싶다고 가정해봅시다.
- \(X \sim N(\mu, \sigma^2)\)이라면 다음 관계(표준화)가 성립합니다.
\[Z = \frac{X - \mu}{\sigma} \sim ~N(0, 1)\]
- 즉, 확률변수 \(X\)를 \(Z\)로 표현한다면 \(X = \mu + \sigma Z\)로 표현할 수 있으며, \((X, Z)\)를 좌표평면에 표시한다고 생각하면 이는 선형이므로 직선관계를 보일 수 있습니다.
- 여기에서는
qqnorm(),qqplot()함수를 이용하여 Q-Q plot을 그릴 수 있고qqline()함수를 사용하여 위에 언급한 두 변수간의 직선관계를 보이는 그림을 그릴 수 있습니다.qqnorm()함수는 하나의 데이터에 Q-Q plot을 출력할 수 있다면,qqplot()은 두 개의 데이터에 대한 Q-Q plot을 출력할 수 있습니다.
x <- rnorm(1000, mean = 10, sd = 1)
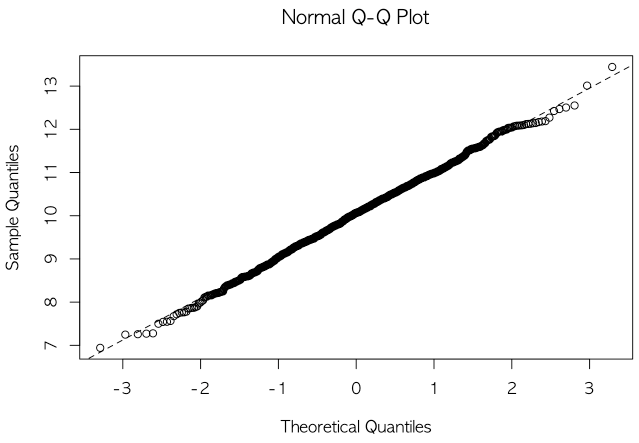
qqnorm(x)
qqline(x, lty = 2)
- 위 그래프처럼 객체 x는 정규분포에서 생성된 샘플이기에 Q-Q plot에서 직선관계가 뚜렷하게 성립함을 볼 수 있습니다.
y <- runif(1000, min = 0, max = 1)
qqnorm(y)
qqline(y, lty = 2)
- 반면에 객체 y는 균일분포에 생성된 샘플이기에 한눈에 봐도 직선 관계가 성립하지 않음을 볼 수 있습니다.
반응형
'Basic' 카테고리의 다른 글
| [R] 추정 및 검정 (0) | 2017.07.12 |
|---|---|
| [R] 상관 분석 (0) | 2017.07.07 |
| [R] 범주형 자료에서 독립성 검정 (0) | 2017.07.04 |
| [R] 표본 추출 (0) | 2017.07.03 |
| [R] 난수생성과 기초통계량 (0) | 2017.07.03 |
TAGS.

