[R] 5. Time-series Regression

library(fpp3)
#library(fable)

The linear model

\[y_{t} = \beta_0 + \beta_1 x_{t} + \epsilon_{t}\]

우리가 흔히 알고 있는 단순선형회귀 모형입니다.
이는 시계열 데이터에 적용할때도 마찬가지로 오차항에 대한 가정을 합니다.
- iid(independent identically distributed)
이를 fable 라이브러리 내 함수를 활용하여 살펴보겠습니다.

예시 데이터는 us_change로 tsibbledata 라이브러리 내에 있습니다.
- 1970년 1분기부터 2019년 2분기까지 미국의 개인 소비 지출(personal consumption expenditure)과 개인 소득(personal disposable income)의 분기별 변화(성장률) 시계열 데이터입니다.

us_change

## # A tsibble: 198 x 6 [1Q]
##    Quarter Consumption Income Production Savings Unemployment
##      <qtr>       <dbl>  <dbl>      <dbl>   <dbl>        <dbl>
##  1 1970 Q1       0.619  1.04      -2.45    5.30         0.9  
##  2 1970 Q2       0.452  1.23      -0.551   7.79         0.5  
##  3 1970 Q3       0.873  1.59      -0.359   7.40         0.5  
##  4 1970 Q4      -0.272 -0.240     -2.19    1.17         0.700
##  5 1971 Q1       1.90   1.98       1.91    3.54        -0.100
##  6 1971 Q2       0.915  1.45       0.902   5.87        -0.100
##  7 1971 Q3       0.794  0.521      0.308  -0.406        0.100
##  8 1971 Q4       1.65   1.16       2.29   -1.49         0    
##  9 1972 Q1       1.31   0.457      4.15   -4.29        -0.200
## 10 1972 Q2       1.89   1.03       1.89   -4.69        -0.100
## # … with 188 more rows

각 변수별 분기 단위의 추이를 살펴보기 위해 tidyr::pivot_longer() 함수를 사용하여 적절히 가공한 후 시각화해보겠습니다.

us_change %>% 
  pivot_longer(
    cols = c("Consumption", "Income"),
    names_to = "Series",
    values_to = "value"
  ) %>% 
  autoplot(value) +
  labs(y = "% change")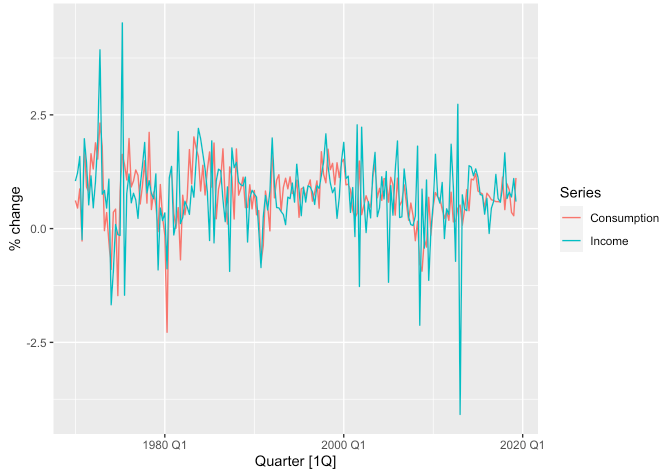

소득과 지출간의 선형관계를 살펴보겠습니다. (geom_smooth(method = "lm") 활용)

us_change %>% 
  ggplot(aes(x = Income, y = Consumption)) +
  geom_point(size = 1.2) +
  geom_smooth(formula = y ~ x, method = "lm", se = FALSE) + # method = "lm"은 linear regerssion을 의미합니다.
  labs(
    x = "Income (quarterly % change)",
    y = "Consumption (quaterly % change)"
  )

같은 방식을 TSLM() 함수를 사용하여 추정해보겠습니다.
결과물 출력은 report() 함수를 활용합니다.

us_change %>% 
  model(TSLM(Consumption ~ Income)) %>% 
  report()

## Series: Consumption 
## Model: TSLM 
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.58236 -0.27777  0.01862  0.32330  1.42229 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.54454    0.05403  10.079  < 2e-16 ***
## Income       0.27183    0.04673   5.817  2.4e-08 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.5905 on 196 degrees of freedom
## Multiple R-squared: 0.1472,  Adjusted R-squared: 0.1429
## F-statistic: 33.84 on 1 and 196 DF, p-value: 2.4022e-08

그 결과 \(\text{Consumption} = 0.54454 + 0.27183\times\text{Income}\) 선형식이 도출되었습니다.
변수의 p-value 값은 유의미하며, 해석을 하자면 소득이 한 단위 증가할 때 지출은 평균적으로 0.27 단위가 증가한다고 볼 수 있습니다.
(절편까지 고려한다면 소득의 1%p 증가는 평균적으로 지출 0.27+0.54 = 0.82%p 증가로 이어짐)

Multiple linear model

\[y_{t} = \beta_0 + \beta_1 x_{1, t} + \beta_2 x_{2, t} + ... + \beta_k x_{k, t} + \epsilon_{t}\]

독립변수가 두 개 이상인 선형 회귀 모형입니다.
바로 예시로 적용해보겠습니다. 소비 지출을 예측하는 데 있어서 개인 소득뿐만 아니라 산업 생산과 개인 저축, 실업률을 포함하여 보고자합니다.

us_change %>% 
  pivot_longer(
    cols = c("Production", "Savings", "Unemployment"),
    names_to = "Series",
    values_to = "value"
  ) %>% 
  autoplot(value, show.legend = FALSE) +
  labs(y = "% change") +
  facet_wrap(. ~ Series, scales = "free_y", nrow = 3)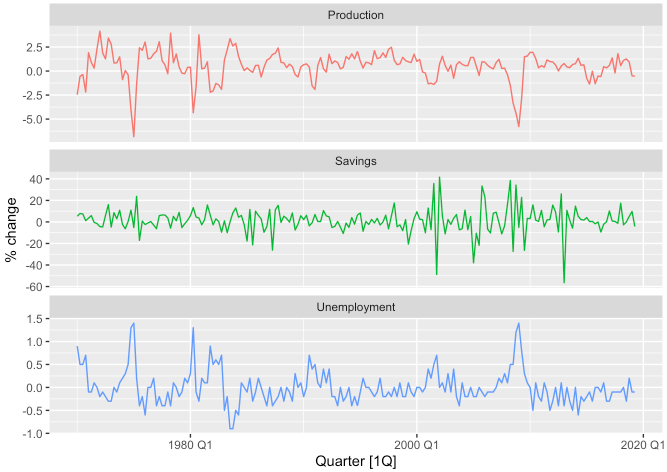

먼저 각 변수들간의 상관관계를 확인하고 싶습니다.
GGally 라이브러리의 ggpairs() 함수를 사용하여 확인할 수 있습니다.

library(GGally)

## Registered S3 method overwritten by 'GGally':
##   method from   
##   +.gg   ggplot2

us_change %>% 
  ggpairs(columns = 2:6)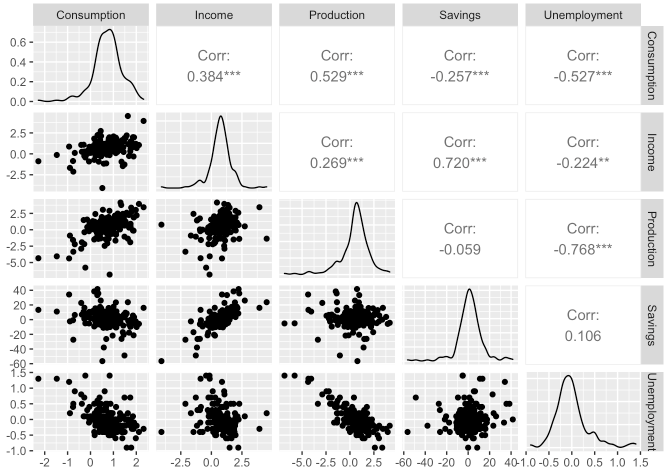

Least Squares Estimation

선형 회귀에서 각 회귀계수 \(\beta_{k}\)의 추정은 아래 오차항의 제곱합을 최소화하는 과정에서 얻어집니다.

\[\sum^{T}_{t=1}\epsilon_{t}^{2} = \sum^{T}_{t=1}\bigg(y_{t} - \beta_0 - \beta_1x_{1,t}-...-\beta_{k}x_{k, t} \bigg)^{2}\]

이 과정을 최소제곱추정이라고 합니다.
TSLM() 함수는 시계열 데이터를 선형회귀모형에 적합시켜줍니다.
물론 가장 널리쓰이는 lm() 함수와 유사하지만 TSLM()은 시계열 처리를 위한 부가 기능이 더 있다고 보시면 될 것 같습니다.
위 예시를 그대로 이어가겠습니다.

fit_consMR <- us_change %>% 
  model(tslm = TSLM(formula = Consumption ~ Income + Production + Unemployment + Savings))

fit_consMR %>% 
  report()

## Series: Consumption 
## Model: TSLM 
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.90555 -0.15821 -0.03608  0.13618  1.15471 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   0.253105   0.034470   7.343 5.71e-12 ***
## Income        0.740583   0.040115  18.461  < 2e-16 ***
## Production    0.047173   0.023142   2.038   0.0429 *  
## Unemployment -0.174685   0.095511  -1.829   0.0689 .  
## Savings      -0.052890   0.002924 -18.088  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3102 on 193 degrees of freedom
## Multiple R-squared: 0.7683,  Adjusted R-squared: 0.7635
## F-statistic:   160 on 4 and 193 DF, p-value: < 2.22e-16

계수에 대한 해석은 다들 아실것이라 생각하고 스킵하겠습니다.

Fitted values

augment() 함수를 사용하여 적합된 값을 출력할 수 있습니다.

fit_consMR %>% 
  augment()

## # A tsibble: 198 x 6 [1Q]
## # Key:       .model [1]
##    .model Quarter Consumption .fitted  .resid  .innov
##    <chr>    <qtr>       <dbl>   <dbl>   <dbl>   <dbl>
##  1 tslm   1970 Q1       0.619   0.474  0.145   0.145 
##  2 tslm   1970 Q2       0.452   0.635 -0.183  -0.183 
##  3 tslm   1970 Q3       0.873   0.931 -0.0583 -0.0583
##  4 tslm   1970 Q4      -0.272  -0.212 -0.0603 -0.0603
##  5 tslm   1971 Q1       1.90    1.64   0.264   0.264 
##  6 tslm   1971 Q2       0.915   1.07  -0.158  -0.158 
##  7 tslm   1971 Q3       0.794   0.658  0.137   0.137 
##  8 tslm   1971 Q4       1.65    1.30   0.347   0.347 
##  9 tslm   1972 Q1       1.31    1.05   0.262   0.262 
## 10 tslm   1972 Q2       1.89    1.37   0.513   0.513 
## # … with 188 more rows

fit_consMR %>% 
  augment() %>% 
  ggplot(aes(x = Quarter)) +
  geom_line(aes(y = Consumption, colour = "Data")) +
  geom_line(aes(y = .fitted, colour = "Fitted")) +
  labs(y = NULL, title = "Percent change in US consumption expenditure") +
  scale_colour_manual(values = c(Data = "black", Fitted = "#D55E00")) +
  guides(colour = guide_legend(title = NULL))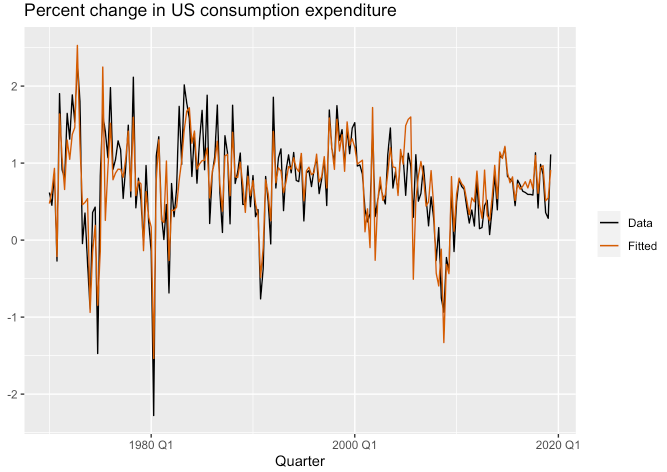

아래 그래프는 예상 소비 지출 대비 실제 소비 지출을 나타낸 산점도 입니다.

fit_consMR %>% 
  augment() %>% 
  ggplot(aes(x = Consumption, y = .fitted)) +
  geom_point(size = 1.2) +
  labs(
    x = "Data (actual values)",
    y = "Fitted (predicted values)",
    title = "Percent change in US consumption expenditure"
  ) +
  geom_abline(intercept = 0, slope = 1, color = "grey50")

Goodness-of-fit

선형 회귀 모형이 데이터에 얼마나 잘 맞는지 요약하는 일반적인 방법은 결정계수(coefficient of determination, \(R^{2}\)) 입니다.
이는 실제 값과 예측 값 사이의 상관관계 제곱으로 계산하거나 아래와 같이 계산할 수 있습니다.

\[R^{2} = \frac{\sum(\hat{y_{t}} - \bar{y})^2}{\sum(y_{t} - \bar{y})^2}\]

해당 값은 0과 1 사이에 위치하여 예측이 실제값과 가까울수록 1에 가까워지는 값을 가집니다.
이는 report() 함수를 통해 결과물을 출력할 때 Adjusted R-squared 값으로 확인할 수 있습니다.

fit_consMR %>% 
  report()

## Series: Consumption 
## Model: TSLM 
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.90555 -0.15821 -0.03608  0.13618  1.15471 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   0.253105   0.034470   7.343 5.71e-12 ***
## Income        0.740583   0.040115  18.461  < 2e-16 ***
## Production    0.047173   0.023142   2.038   0.0429 *  
## Unemployment -0.174685   0.095511  -1.829   0.0689 .  
## Savings      -0.052890   0.002924 -18.088  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3102 on 193 degrees of freedom
## Multiple R-squared: 0.7683,  Adjusted R-squared: 0.7635
## F-statistic:   160 on 4 and 193 DF, p-value: < 2.22e-16

Standard error of the regression

모형이 데이터를 얼마나 잘 적합시켰는지에 대한 또 다른 평가는 잔차의 표준 오차로 알려진 잔차 표준 편차입니다.

\[\hat{\sigma_{e}} = \sqrt{\frac{1}{T-k-1}\sum^{T}_{t=1}e_{t}^2}\]

이 또한 report() 함수를 통해 결과물을 출력할 때 Residual standard error 값으로 확인할 수 있습니다.

Evaluating the regression model

회귀 모형 적합 이후에는 모형의 가정이 충족되었는지 확인하기 위해 잔차항을 체크해야합니다.

ACF plot of residuals & Histogram of residuals

시계열 데이터의 경우 현재 t시점의 값이 이전 t-1 시점 또는 그 이전 기간의 값과 유사하거나 영향을 받을 가능성이 매우 높습니다.
따라서 시계열 데이터를 회귀 모형에 적합시킬 때는 잔차항에서 자기 상관을 찾는 것이 일반적입니다.
자기 상관이 있는 모델의 예측은 편향은 없기에 틀림이라고 볼 수는 없지만, 일반적으로 더 갭이 큰 예측 오차를 가질 가능성이 높습니다.
또한 잔차가 정규 분포를 따르는 지 확인해야 합니다.
gg_tsresiduals() 함수를 통해 잔차항에 대한 진단을 해볼 수 있습니다.

fit_consMR %>% 
  gg_tsresiduals()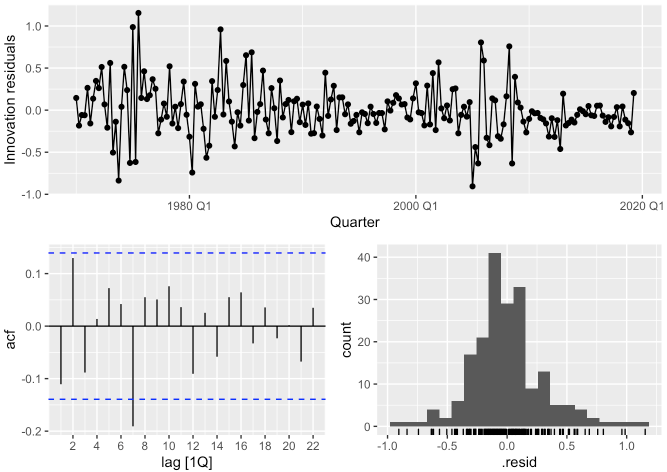

fit_consMR %>% 
  augment() %>% 
  features(
    .var = .innov,
    features = ljung_box,
    lag = 10, 
    dof = 5
  )

## # A tibble: 1 x 3
##   .model lb_stat lb_pvalue
##   <chr>    <dbl>     <dbl>
## 1 tslm      18.9   0.00204

자기상관함수 그래프에서 시차 7에 벗어나는 점을 보이지만 크게 영향을 미치지 않을 수도 있습니다.

Residual plots against predictors

각 변수에 대해 산점도를 체크해볼 필요도 있습니다.

fit_consMR %>% 
  residuals()

## # A tsibble: 198 x 3 [1Q]
## # Key:       .model [1]
##    .model Quarter  .resid
##    <chr>    <qtr>   <dbl>
##  1 tslm   1970 Q1  0.145 
##  2 tslm   1970 Q2 -0.183 
##  3 tslm   1970 Q3 -0.0583
##  4 tslm   1970 Q4 -0.0603
##  5 tslm   1971 Q1  0.264 
##  6 tslm   1971 Q2 -0.158 
##  7 tslm   1971 Q3  0.137 
##  8 tslm   1971 Q4  0.347 
##  9 tslm   1972 Q1  0.262 
## 10 tslm   1972 Q2  0.513 
## # … with 188 more rows

us_change %>% 
  left_join(residuals(fit_consMR), by = "Quarter") %>% 
  pivot_longer(
    cols = Income:Unemployment,
    names_to = "regressor",
    values_to = "x"
  ) %>% 
  ggplot(aes(x = x, y = .resid)) +
  geom_point(size = 1.2) +
  facet_wrap(. ~ regressor, scales = "free_x") +
  labs(x = NULL, y = "Residuals")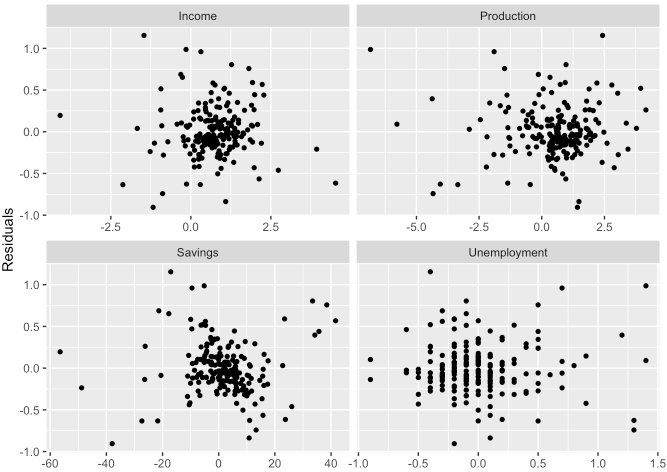

위 그래프에서 보이다시피 각 변수별 잔차가 무작위로 흩어져 분포되어 있는 것처럼 보이므로 어느 정도 가정을 만족한다고 볼 수 있습니다.

Residual plots against fitted values

적합된 값과 잔차간의 분포에도 특별한 패턴이 보이면 안됩니다.
패턴이 관찰되면 오차에 등분산성 가정이 위배될 가능성이 있기 때문입니다.
이렇게 등분산성 가정이 만족하지 못할 경우 로그 또는 제곱근과 같이 변수의 변환을 주어야할 수도 있습니다.

fit_consMR %>% 
  augment() %>% 
  ggplot(aes(x = .fitted, y = .resid)) +
  geom_point(size = 1.2) +
  labs(x = "Fitted", y = "Residuals")

어느 특정한 패턴이 보이지 않으므로 등분산성을 만족한다고 볼 수 있습니다.

Outliers and influential observations

대부분의 관측값과 비교하여 극단적인 값을 취하는 값을 이상치라고 합니다.
회귀 모델의 추정 계수에 큰 영향을 미치는 관측치는 영향력 있는 관측치(influential observations)라고 합니다.
일반적으로 영향력 있는 관측치는 극단의 이상치일 가능성도 있습니다.
이러한 이상치들을 무조건 제거한다고 그게 올바르다고 보기는 어렵습니다.
이상치여도 의미 있는 값이 있을수도 있기에, 그 값이 가능한 이유에 대해서 분석하는 것이 중요합니다.

Spurious regression

시계열 데이터는 종종 정상성(stationarity)을 보이지 않는 경우도 있습니다.
- 시간이 지나도 분산이 일정한.. 즉, 시계열의 변동이 시간의 흐름에 따라 일정한 것을 정상성이라고 이해하시면 됩니다.
이렇게 비정상 시계열은 정상 시계열로 변환해줄 필요가 있습니다.
비정상 시계열을 회귀 모형에 적합하면 부정확한 모형이 될 가능성이 있기 때문입니다.

temp_fit <- aus_airpassengers %>% 
  filter(Year <= 2011) %>% 
  left_join(guinea_rice, by = "Year") %>% 
  model(TSLM(Passengers ~ Production))

temp_fit %>% 
  report()

## Series: Passengers 
## Model: TSLM 
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -5.9448 -1.8917 -0.3272  1.8620 10.4210 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   -7.493      1.203  -6.229 2.25e-07 ***
## Production    40.288      1.337  30.135  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.239 on 40 degrees of freedom
## Multiple R-squared: 0.9578,  Adjusted R-squared: 0.9568
## F-statistic: 908.1 on 1 and 40 DF, p-value: < 2.22e-16

temp_fit %>% 
  gg_tsresiduals()

Some useful predictors

Trend

\[y_{t} = \beta_{0} + \beta_{1} t + \epsilon_{t}\]

TSLM() 함수에는 trend()를 적용하여 추세 변수를 지정할 수 있습니다.

Dummy variables

예를 들어 시계열 데이터에서 어떤 특정 날짜가 공휴일인지 여부를 고려할 때 변수에 공휴일이면 1, 아니면 0 과 같이 값을 취할 수 있습니다.
이를 더미 변수라고 하며 Indicator variable이라고도 불리웁니다.
범주가 세 개 이상인 k개일 경우에는 (k-1)개의 변수를 더미처리하여 사용할 수 있습니다.
TSLM() 함수에서는 더미 지정하면 이를 자동으로 처리해줍니다.

Seasonal dummy variables

계절성을 갖는 더미 변수(요일, 분기 등)도 마찬가지로 TSLM() 함수 내 season()을 적용하여 지정할 수 있습니다.
아래 예시를 들어 확인해보겠습니다. (호주의 분기별 맥주 생산량 데이터)

recent_production <- aus_production %>% 
  filter(year(Quarter) >= 1992)

recent_production %>% 
  autoplot(Beer) +
  labs(y = "Megalitres", title = "Australian quarterly beer production")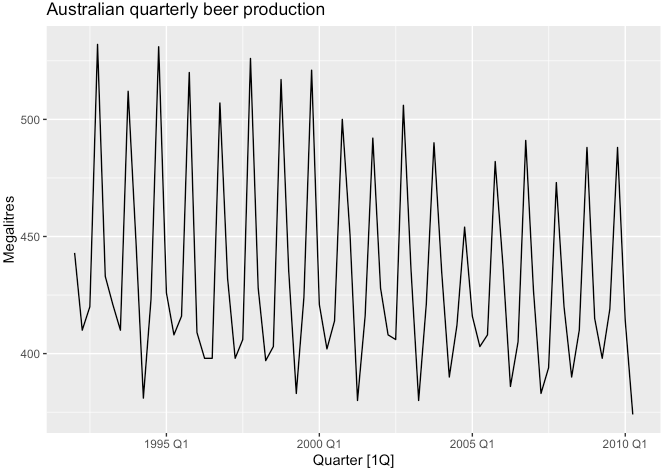

미래의 맥주 생산량을 확인해보고 싶습니다.
선형 추세(trend)와 더미 변수가 있는 회귀 모형을 사용하여 모델링할 수 있습니다.
- 분기 데이터이기에 더미는 세 개가 됩니다. (4-1 = 3)

\[y_{t} = \beta_{0} + \beta_{1}t + \beta_{2}t_{2, t} + \beta_{3}t_{3, t} + \beta_{4}t_{4, t} + \epsilon_t\]

# trend() 함수와 season() 함수는 디폴트로 들어가는 표준함수가 아닙니다. 필요 시 TSLM() 함수 안에서 적용합니다.
fit_beer <- recent_production %>% 
  model(TSLM(formula = Beer ~ trend() + season()))

fit_beer %>% 
  report()

## Series: Beer 
## Model: TSLM 
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -42.9029  -7.5995  -0.4594   7.9908  21.7895 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   441.80044    3.73353 118.333  < 2e-16 ***
## trend()        -0.34027    0.06657  -5.111 2.73e-06 ***
## season()year2 -34.65973    3.96832  -8.734 9.10e-13 ***
## season()year3 -17.82164    4.02249  -4.430 3.45e-05 ***
## season()year4  72.79641    4.02305  18.095  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 12.23 on 69 degrees of freedom
## Multiple R-squared: 0.9243,  Adjusted R-squared: 0.9199
## F-statistic: 210.7 on 4 and 69 DF, p-value: < 2.22e-16

적합된 결과를 확인해보면 분기당 평균 -0.34 감소 추세가 있습니다.
평균적으로 2분기는 1분기보다 -34.7, 3분기는 1분기보다 -17.8, 반면 4분기는 1분기보다 72.8 정도 생산량이 많습니다.

fit_beer %>% 
  augment() %>% 
  ggplot(aes(x = Quarter)) +
  geom_line(aes(y = Beer, colour = "Data")) +
  geom_line(aes(y = .fitted, colour = "Fitted")) +
  scale_colour_manual(values = c(Data = "black", Fitted = "#D55E00")) +
  labs(y = "Megalitres", title = "Australian quarterly beer production") +
  guides(colour = guide_legend(title = "Series"))

아래 그래프와 같이 분기별 실제 맥주 생산량과 예상치를 표현해볼 수도 있습니다.

fit_beer %>% 
  augment() %>% 
  ggplot(aes(x = Beer, y = .fitted, colour = factor(quarter(Quarter)))) +
  geom_point(size = 1.2) +
  labs(x = "Actual values", y = "Fitted", title = "Australian quarterly beer production") +
  geom_abline(intercept = 0, slope = 1) +
  guides(colour = guide_legend(title = "Quarter"))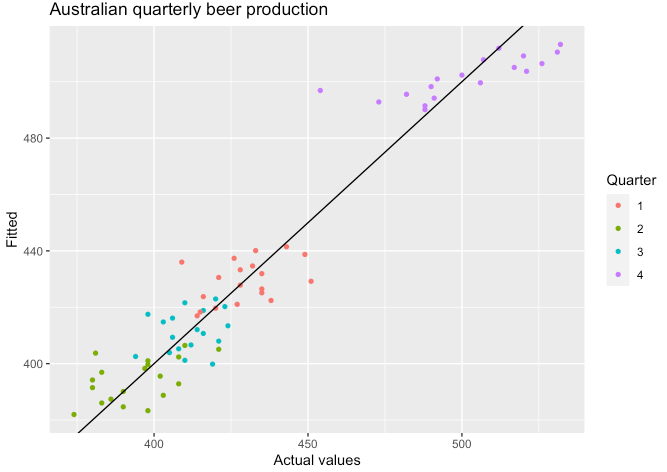

Intervention variables

종속 변수에 영향을 줄 수 있는 변수들을 개입하는 것이 종종 필요할 수도 있습니다.
예를 들자면 특정 프로모션 기간 전후에 차이가 있다고 가정할 때 프로모션 전에는 0, 후에는 1과 같이 더미처럼 변수 개입을 주는 것입니다.
이러한 개입은 piecewise linear trend가 되기에 기울기의 변화가 발생하게 되고, 이는 즉 비선형에 해당되게 됩니다.

Fourier series

긴 계절 기간 동안 계절 더미 변수를 사용할 때 대안 중 하나는 푸리에(Fourier) 항을 사용하는 것입니다.
\(m\) = seasonal period
- \(x_{1, t} = \sin\big(\frac{2\pi t}{m}\big)\)
- \(x_{2, t} = \cos\big(\frac{2\pi t}{m}\big)\)
- \(x_{3, t} = \sin\big(\frac{4\pi t}{m}\big)\)
- \(x_{4, t} = \cos\big(\frac{4\pi t}{m}\big)\)
- \(x_{5, t} = \sin\big(\frac{6\pi t}{m}\big)\)
- \(x_{6, t} = \cos\big(\frac{6\pi t}{m}\big)\)
- …
푸리에 항을 사용하면 더미 변수가 줄어들 수 있는 이점을 갖습니다.
예를 들자면 시계열이 주간 단위로 되어 있는 케이스 등이 될 것 같습니다. (\(m = 52\))
이러한 푸리에 항은 fourier() 함수로 적용할 수 있습니다.
- K arguments는 몇개의 sin, cos 항을 포함시킬지 결정하는 부분
- \(m\)이 계절 주기라고 할 때 허용되는 \(K\)의 최대값은 \(K = m/2\)
- 분기별 데이터이므로 \(m=4\)이기에 여기서는 \(K=2\)

recent_production %>% 
  model(TSLM(formula = Beer ~ trend() + fourier(K = 2))) %>% 
  report()

## Series: Beer 
## Model: TSLM 
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -42.9029  -7.5995  -0.4594   7.9908  21.7895 
## 
## Coefficients:
##                     Estimate Std. Error t value Pr(>|t|)    
## (Intercept)        446.87920    2.87321 155.533  < 2e-16 ***
## trend()             -0.34027    0.06657  -5.111 2.73e-06 ***
## fourier(K = 2)C1_4   8.91082    2.01125   4.430 3.45e-05 ***
## fourier(K = 2)S1_4 -53.72807    2.01125 -26.714  < 2e-16 ***
## fourier(K = 2)C2_4 -13.98958    1.42256  -9.834 9.26e-15 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 12.23 on 69 degrees of freedom
## Multiple R-squared: 0.9243,  Adjusted R-squared: 0.9199
## F-statistic: 210.7 on 4 and 69 DF, p-value: < 2.22e-16

Selecting predictors

회귀 모형 적합 이후 변수를 선별할 때 우리는 흔히 p-value 값이 일정 유의수준 이하인 경우를 채택했습니다.
하지만 이렇게 p-value의 통계적 유의성이 항상 맞고 옳다고는 보기 어렵습니다.
두 개 이상의 변수가 서로 상관 관계가 있을 경우에 p-value로의 판단은 잘못된 판단이 될 수도 있기 때문입니다.
이러한 오차를 최소화하기 위해 변수 클렌징이 다 된 최종 모형에 대한 평가를 고려해볼 수 있습니다.
glance() 함수는 이러한 값을 제공해줍니다.

fit_consMR %>% 
  glance() %>% 
  select(adj_r_squared, CV, AIC, AICc, BIC)

## # A tibble: 1 x 5
##   adj_r_squared    CV   AIC  AICc   BIC
##           <dbl> <dbl> <dbl> <dbl> <dbl>
## 1         0.763 0.104 -457. -456. -437.

Adjusted R-squared

일반적인 \(R^2\) 값은 모형이 과거 데이터에 얼마나 잘 맞는지를 측정하지만, 미래에 예측을 얼마나 잘하는지는 측정하지 않습니다.
또한 자유도(degree of freedom) 항을 고려하지 않기에 변수가 많을수록 \(R^2\) 값은 증가하는 경향이 있습니다.
따라서 이렇게 자유도 항을 고려한 것이 Adjusted R-squared 입니다.
- 우리말로는 조정된 결정계수 또는 수정된 결정계수 라고도 부르는 것 같습니다.
이 값을 최대화하는 것은 모델 오차항의 표준오차 \(\sigma_{e}\)를 최소화하는 것과 같습니다.

Cross-validation

설명이 길어지기에 일단 교차검증에 대한 위키 백과 링크를 첨부드립니다.
시계열에서도 마찬가지로 교차 검증은 모델의 예측력을 평가하기 위한 일반적인 방법입니다.
이 값이 작을수록 좋은 모형이라고 평가할 수 있습니다.

Akaike’s Information Criterion

\[\text{AIC} = T \log\bigg(\frac{\text{SSE}}{T}\bigg) + 2(k+2)\]

\(T\)는 관측치의 수, \(k\)는 변수의 수 입니다.
마찬가지로 작은 값을 가질수록 가장 적합한 모형이라고 평가할 수 있습니다.
AIC를 최소화하는 것은 CV를 최소화하는 것과 동일한 맥락이라고 볼 수 있습니다.

Corrected Akaike’s Information Criterion

관측치의 수 \(T\)가 작을 때 AIC는 너무 많은 예측 변수를 선택하는 경향이 있으므로 아래와 같이 수정된 버전입니다.

\[\text{AIC}_{c} = \text{AIC} + \frac{2(k+2)(k+3)}{T-k-3}\]

마찬가지로 작을수록 베스트입니다.

Schwarz’s Bayesian Information Criterion

\[\text{BIC} = T\log\bigg(\frac{\text{SSE}}{T}\bigg) + (k+2)\log(T)\]

AIC와 동일한 맥락으로 BIC를 최소화하는 것이 좋습니다.

Which measure should we use?

관련 문서에서는 AICc, AIC 또는 CV 통계량 중 하나를 사용하는 것을 추천합니다.
길지 않으니 관련 문서를 꼭 한 번 읽어보시길 권장드립니다.
대부분의 예시들에서도 AICc 값으로 예측 모형을 선택하겠습니다.

Forecasting with regression

TSLM() 함수에 적합된 객체를 가지고 forecast() 함수를 적용하여 예측을 해볼 수 있습니다.

fit_beer %>% 
  report()

## Series: Beer 
## Model: TSLM 
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -42.9029  -7.5995  -0.4594   7.9908  21.7895 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   441.80044    3.73353 118.333  < 2e-16 ***
## trend()        -0.34027    0.06657  -5.111 2.73e-06 ***
## season()year2 -34.65973    3.96832  -8.734 9.10e-13 ***
## season()year3 -17.82164    4.02249  -4.430 3.45e-05 ***
## season()year4  72.79641    4.02305  18.095  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 12.23 on 69 degrees of freedom
## Multiple R-squared: 0.9243,  Adjusted R-squared: 0.9199
## F-statistic: 210.7 on 4 and 69 DF, p-value: < 2.22e-16

fc_beer <- fit_beer %>% 
  forecast()

fc_beer

## # A fable: 8 x 4 [1Q]
## # Key:     .model [1]
##   .model                                    Quarter        Beer .mean
##   <chr>                                       <qtr>      <dist> <dbl>
## 1 TSLM(formula = Beer ~ trend() + season()) 2010 Q3 N(398, 164)  398.
## 2 TSLM(formula = Beer ~ trend() + season()) 2010 Q4 N(489, 164)  489.
## 3 TSLM(formula = Beer ~ trend() + season()) 2011 Q1 N(416, 165)  416.
## 4 TSLM(formula = Beer ~ trend() + season()) 2011 Q2 N(381, 165)  381.
## 5 TSLM(formula = Beer ~ trend() + season()) 2011 Q3 N(397, 166)  397.
## 6 TSLM(formula = Beer ~ trend() + season()) 2011 Q4 N(487, 166)  487.
## 7 TSLM(formula = Beer ~ trend() + season()) 2012 Q1 N(414, 166)  414.
## 8 TSLM(formula = Beer ~ trend() + season()) 2012 Q2 N(379, 166)  379.

그 결과를 시각화로 표현한 결과는 아래와 같습니다.
- 음영으로 된 구간중 어두운 음영은 예측 80% 신뢰구간, 조금 더 밝은 음영은 95% 신뢰구간을 나타냅니다.

fc_beer %>% 
  autoplot(recent_production) +
  labs(y = "megalitres", title = "Forecasts of beer production using regression")

이번엔 다른 데이터인 us_change로 시나리오 기반 예측을 해보겠습니다.

us_change

## # A tsibble: 198 x 6 [1Q]
##    Quarter Consumption Income Production Savings Unemployment
##      <qtr>       <dbl>  <dbl>      <dbl>   <dbl>        <dbl>
##  1 1970 Q1       0.619  1.04      -2.45    5.30         0.9  
##  2 1970 Q2       0.452  1.23      -0.551   7.79         0.5  
##  3 1970 Q3       0.873  1.59      -0.359   7.40         0.5  
##  4 1970 Q4      -0.272 -0.240     -2.19    1.17         0.700
##  5 1971 Q1       1.90   1.98       1.91    3.54        -0.100
##  6 1971 Q2       0.915  1.45       0.902   5.87        -0.100
##  7 1971 Q3       0.794  0.521      0.308  -0.406        0.100
##  8 1971 Q4       1.65   1.16       2.29   -1.49         0    
##  9 1972 Q1       1.31   0.457      4.15   -4.29        -0.200
## 10 1972 Q2       1.89   1.03       1.89   -4.69        -0.100
## # … with 188 more rows

여기서 시나리오는 아래와 같이 셋팅합니다.
- 고용률(Unemployment 관련)의 변화 없이 소득(Income)과 저축(Savings)이 각각 1%와 0.5%로 증가하거나 감소
- 예측을 위한 시나리오 셋팅은 scenarios() 함수를 통해 구성해볼 수 있습니다.
tsibble 라이브러리 내 new_data() 함수는 key-index 조합으로 원하는 시점만큼의 미래 값을 생성해주는 함수입니다.

# 회귀모형 적합
fit_consBest <- us_change %>% 
  model(lm = TSLM(formula = Consumption ~ Income + Savings + Unemployment))

# 시나리오 구성
future_scenarios <- scenarios(
  Increase = new_data(us_change, 4) %>% 
    mutate(
      Income = 1,
      Savings = 0.5,
      Unemployment = 0
    ),
  Decrease = new_data(us_change, 4) %>% 
    mutate(
      Income = -1,
      Savings = -0.5,
      Unemployment = 0
    ),
  names_to = "Scenario"
)

future_scenarios

## $Increase
## # A tsibble: 4 x 4 [1Q]
##   Quarter Income Savings Unemployment
##     <qtr>  <dbl>   <dbl>        <dbl>
## 1 2019 Q3      1     0.5            0
## 2 2019 Q4      1     0.5            0
## 3 2020 Q1      1     0.5            0
## 4 2020 Q2      1     0.5            0
## 
## $Decrease
## # A tsibble: 4 x 4 [1Q]
##   Quarter Income Savings Unemployment
##     <qtr>  <dbl>   <dbl>        <dbl>
## 1 2019 Q3     -1    -0.5            0
## 2 2019 Q4     -1    -0.5            0
## 3 2020 Q1     -1    -0.5            0
## 4 2020 Q2     -1    -0.5            0
## 
## attr(,"names_to")
## [1] "Scenario"

이러한 시나리오 구성을 forecast() 함수 내 new_data argument에 적용합니다.

fc <- fit_consBest %>% 
  forecast(new_data = future_scenarios)

fc

## # A fable: 8 x 8 [1Q]
## # Key:     Scenario, .model [2]
##   Scenario .model Quarter   Consumption  .mean Income Savings Unemployment
##   <chr>    <chr>    <qtr>        <dist>  <dbl>  <dbl>   <dbl>        <dbl>
## 1 Increase lm     2019 Q3   N(1, 0.098)  0.996      1     0.5            0
## 2 Increase lm     2019 Q4   N(1, 0.098)  0.996      1     0.5            0
## 3 Increase lm     2020 Q1   N(1, 0.098)  0.996      1     0.5            0
## 4 Increase lm     2020 Q2   N(1, 0.098)  0.996      1     0.5            0
## 5 Decrease lm     2019 Q3 N(-0.46, 0.1) -0.464     -1    -0.5            0
## 6 Decrease lm     2019 Q4 N(-0.46, 0.1) -0.464     -1    -0.5            0
## 7 Decrease lm     2020 Q1 N(-0.46, 0.1) -0.464     -1    -0.5            0
## 8 Decrease lm     2020 Q2 N(-0.46, 0.1) -0.464     -1    -0.5            0

이를 가지고 autolayer() 함수에 시나리오 예측 적용 객체를 씌워주어 아래와 같이 시각화 해볼 수 있습니다.

us_change %>% 
  autoplot(Consumption) +
  autolayer(fc) +
  labs(title = "US consumption", y = "% change")

Nonlinear regression

일반적인 모형의 수식 형태는 아래와 같습니다.

\[y_{t} = f(x_{t})+\epsilon_{t}\]

여기서 함수 \(f()\)는 비선형함수를 고려합니다.
- 가장 단순한 형태의 \(f()\) 함수는 piecewise linear 포맷이 있을 수 있습니다.
- regression splines 스플라인 회귀도 있습니다.
- 2차항 이상의 고차항 함수를 적용하거나 자연로그 (변수 값들이 양수 이상 일때) 등을 씌우는 방법도 있습니다.
아래 예시를 들어 보겠습니다.

boston_men <- boston_marathon %>% 
  filter(Year >= 1924 & Event == "Men's open division") %>% 
  mutate(Minutes = as.numeric(Time)/60)

boston_men

## # A tsibble: 96 x 6 [1Y]
## # Key:       Event [1]
##    Event              Year Champion               Country      Time      Minutes
##    <fct>             <int> <chr>                  <chr>        <drtn>      <dbl>
##  1 Men's open divis…  1924 Clarence H. DeMar      United Stat…  8980 se…    150.
##  2 Men's open divis…  1925 Charles L. (Chuck) Me… United Stat…  9180 se…    153 
##  3 Men's open divis…  1926 John C. Miles          Canada        8740 se…    146.
##  4 Men's open divis…  1927 Clarence H. DeMar      United Stat…  9622 se…    160.
##  5 Men's open divis…  1928 Clarence H. DeMar      United Stat…  9427 se…    157.
##  6 Men's open divis…  1929 John C. Miles          Canada        9188 se…    153.
##  7 Men's open divis…  1930 Clarence H. DeMar      United Stat…  9288 se…    155.
##  8 Men's open divis…  1931 James P. Henigan       United Stat… 10005 se…    167.
##  9 Men's open divis…  1932 Paul de Bruyn          Germany       9216 se…    154.
## 10 Men's open divis…  1933 Leslie S. Pawson       United Stat…  9061 se…    151.
## # … with 86 more rows

boston_men %>% 
  autoplot(Minutes) +
  geom_smooth(formula = y ~ x, se = FALSE, method = "lm") +
  labs(x = "Year", y = "Minutes")

boston_men %>% 
  model(TSLM(formula = Minutes ~ trend())) %>% 
  gg_tsresiduals()

위 그래프에서 시간이 지남에 따라 감소하는 듯한 선형 추이를 보이지만,
선형추세로 나온 잔차를 보면 비선형 패턴이 보여지게 됩니다.
따라서 아래 코드와 같이 자연로그 또는 piecewise reg. 등을 적합시켜 비교해보겠습니다.

fit_trends <- boston_men %>% 
  model(
    linear = TSLM(formula = Minutes ~ trend()),
    exponential = TSLM(formula = log(Minutes) ~ trend()),
    piecewise = TSLM(formula = Minutes ~ trend(knots = c(1950, 1980)))
  )

fc_trends <- fit_trends %>% 
  forecast(h = 10)

boston_men %>% 
  autoplot(Minutes) +
  geom_line(data = fit_trends %>% fitted(), aes(y = .fitted, colour = .model)) +
  autolayer(fc_trends, alpha = 0.5, level = 95) +
  labs(y = "Minutes", title = "Boston marathon winning times")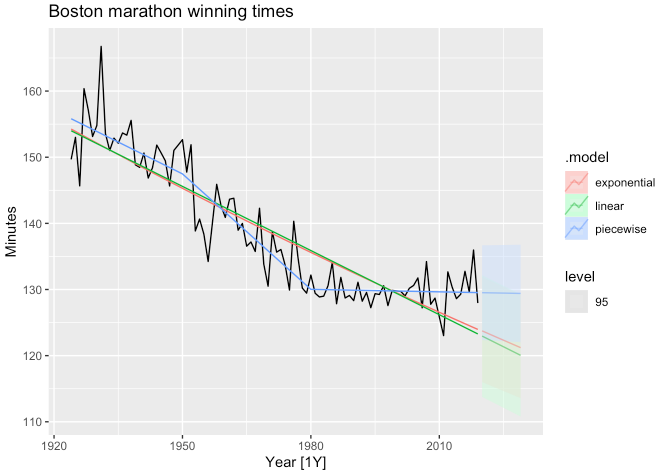

가장 베스트는 piecewise reg.에서 도출될 것 같습니다.

저작자표시 비영리

'time-series (tidy approach)' 카테고리의 다른 글

[R] 7. ARIMA (AutoRegressive Integrated Moving Average) (0)	2021.08.06
[R] 6. Exponential smoothing (0)	2021.07.29
[R] 4. feasts (0)	2021.07.28
[R] 3. tsibbledata (0)	2021.07.28
[R] 2. tsibble (0)	2021.07.27

TAGS.

제이드의 낙서장

카테고리

방문자수