[R] 6. Exponential smoothing
library(fpp3)
#library(fable)Simple exponential smoothing
- SES(Simple Exponential Smoothing)는 지수 평활화 방법 중 가장 단순한 방법입니다.
- 이 방법은 뚜렷한 추세나 계절적 패턴이 없는 데이터를 예측하는데 적합합니다.
- SES와 같이 나이브한 방법을 사용하면 미래에 대한 모든 예측값은 시계열의 마지막 관측값과 같습니다.
- 따라서 예측 시점을 기준으로 가장 최근의 관측치가 유일하게 중요한 관측치이면서 그 이전 관측치는 미래에 대한 정보를 제공하지 않는다고 가정합니다.
- 즉, 모든 가중치가 마지막 관측치에 주어지는 가중 평균으로 생각할 수 있습니다.
\[\hat{y}_{T+h|T} = \frac{1}{T}\sum^{T}_{t=1}y_{t}\] - 그러나 먼 과거의 관측치보다 최그 관측치에 더 큰 가중치를 부여하는 것이 현명할 수 있습니다. - 이것이 바로 SES의 개념입니다. - 예측값은 가중 평균을 사용하여 계산하되, 관측치가 더 먼 과거에서 올수록 가중치가 지수적으로 감소하게 되는 형태입니다.
\[\hat{Y}_{T+1|T} = \alpha y_{T} + \alpha(1-\alpha)y_{T-1} + \alpha(1-\alpha)^{2}y_{T-2} + ...\]
- 위 식에서 \(\alpha\)는 0과 1 사이의 값을 갖는 smoohting parameter 이며 가중치가 감소하는 비율은 이 매개변수에 의해 제어됩니다.
- 더 자세한 수식 전개는 다루지 않겠습니다.
- SES는 평평한 예측(Flat forecasts)이 가능합니다.
즉, 모든 예측은 마지막 관측치 요소와 동일한 수준의 값을 취합니다. - 이러한 예측은 시계열의 추세나 계절 성분이 없는 경우에만 적합하다는 것을 참고하세요!
\[\hat{y}_{T+h|T} = \hat{y}_{T+1|T} = l_{T}\]
Optimisation
- 회귀 모형에서 잔차제곱합을 최소화하여 회귀 모델의 계수를 추정하는 것처럼 이도 유사하게 아래 SSE 값을 최소화하여 추정합니다.
- 물론 unknown parameter인 \(\alpha\)는 분석가가 사전에 셋팅해야합니다.
\[\text{SSE} = \sum^{T}_{t=1}\bigg(y_{t} - \hat{y}_{t|t-1}\bigg)^{2} = \sum^{T}_{t=1}\epsilon_{t}^{2}\]
- 예시를 위해 아래와 같이
tsibbledata라이브러리의global_economy데이터를 사용할 것입니다.
algeria_economy <- global_economy %>%
filter(Country == "Algeria")
algeria_economy %>%
autoplot(Exports) +
labs(y = "% of GDP", title = "Exports: Algeria")
- 지수평활화를 적용하는 함수는
ETS()입니다.- 추세, 계절, 에러 등 각 항별로 수식의 폼을 정할 수 있습니다.
- “A”: Additive (가법) " “M”: Multiplicative (승법)
- “Ad”, “Md”: 감쇠방법
- “N”: None
# 추세와 계절성이 없기에 method arguments는 "N"
fit <- algeria_economy %>%
model(ETS(formula = Exports ~ error("A") + trend("N") + season("N")))
fit %>%
report()## Series: Exports
## Model: ETS(A,N,N)
## Smoothing parameters:
## alpha = 0.8399875
##
## Initial states:
## l[0]
## 39.539
##
## sigma^2: 35.6301
##
## AIC AICc BIC
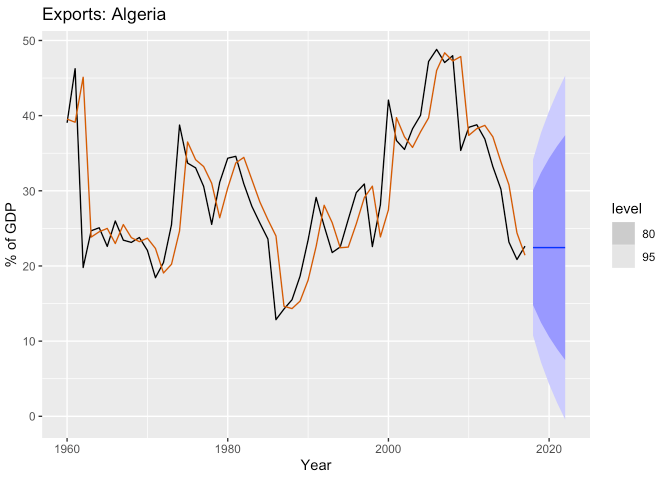
## 446.7154 447.1599 452.8968- smoothing parameter \(\alpha\)는 대략 0.84이며 SSE를 최소화하면서 얻어진 초기값은 39.5입니다.
fc <- fit %>%
forecast(h = 5)
fc %>%
autoplot(algeria_economy) +
geom_line(data = fit %>% augment(), aes(y = .fitted), color = "#D55E00") +
labs(y = "% of GDP", title = "Exports: Algeria")
Methods with trend
Holt’s linear trend method
- 추세가 있는 시계열 데이터를 단순 지수 평활에 적용하기 위해 확장한 방법이 있습니다.
- 이 방법에는 예측 방정시과 두 개의 평활 방정식이 포함됩니다.
- Forecast equation = \(\hat{y}_{t+h|t} = l_t + hb_{t}\)
- Level equation = \(l_{t} = \alpha y_{t} + (1-\alpha)(l_{t-1}+b_{t-1})\)
- Trend equation = \(b_{t} = \beta^{*}(l_{t} - l_{t-1})+(1-\beta^{*})b_{t-1}\)
- \(l_{t}\)는 \(t\)시점에서의 level 추정치이고, \(b_{t}\)는 트렌드(기울기) 추정치입니다.
- 마찬가지로 각각의 smoothing parameter인 \(\alpha\)와 \(\beta^{*}\)는 0과 1사이의 값을 갖습니다.
- 이렇게 추정하면 예측 함수는 더 이상 평평하지 않고 어느 정도 트렌드를 타게됩니다.
- 아래 예시는 1960년부터 2017년까지 호주의 연간 인구수를 보여줍니다.
aus_economy <- global_economy %>%
filter(Code == "AUS") %>%
mutate(Pop = Population / 1000000)
aus_economy## # A tsibble: 58 x 10 [1Y]
## # Key: Country [1]
## Country Code Year GDP Growth CPI Imports Exports Population Pop
## <fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 Australia AUS 1960 1.86e10 NA 7.96 14.1 13.0 10276477 10.3
## 2 Australia AUS 1961 1.96e10 2.49 8.14 15.0 12.4 10483000 10.5
## 3 Australia AUS 1962 1.99e10 1.30 8.12 12.6 13.9 10742000 10.7
## 4 Australia AUS 1963 2.15e10 6.21 8.17 13.8 13.0 10950000 11.0
## 5 Australia AUS 1964 2.38e10 6.98 8.40 13.8 14.9 11167000 11.2
## 6 Australia AUS 1965 2.59e10 5.98 8.69 15.3 13.2 11388000 11.4
## 7 Australia AUS 1966 2.73e10 2.38 8.98 15.1 12.9 11651000 11.7
## 8 Australia AUS 1967 3.04e10 6.30 9.29 13.9 12.9 11799000 11.8
## 9 Australia AUS 1968 3.27e10 5.10 9.52 14.5 12.3 12009000 12.0
## 10 Australia AUS 1969 3.66e10 7.04 9.83 13.3 12.0 12263000 12.3
## # … with 48 more rowsaus_economy %>%
autoplot(Pop) +
labs(y = "Millions", title = "Australian population")
- 여기의 Holt’s linear trend method를 적용하겠습니다.
- 마찬가지로
ETS()함수를 쓰되 추세항에 Additive 옵션을 줍니다.
fit <- aus_economy %>%
model(AAN = ETS(formula = Pop ~ error("A") + trend("A") + season("N")))
fit %>%
report()## Series: Pop
## Model: ETS(A,A,N)
## Smoothing parameters:
## alpha = 0.9999
## beta = 0.3266366
##
## Initial states:
## l[0] b[0]
## 10.05414 0.2224818
##
## sigma^2: 0.0041
##
## AIC AICc BIC
## -76.98569 -75.83184 -66.68347- \(\hat{\alpha} = 0.9999\), \(\hat{\beta^{*}} = 0.3266\)
fc <- fit %>%
forecast(h = 5)
fc %>%
autoplot(aus_economy) +
geom_line(data = fit %>% augment(), aes(y = .fitted), color = "#D55E00") +
labs(y = "Millions", title = "Australian population")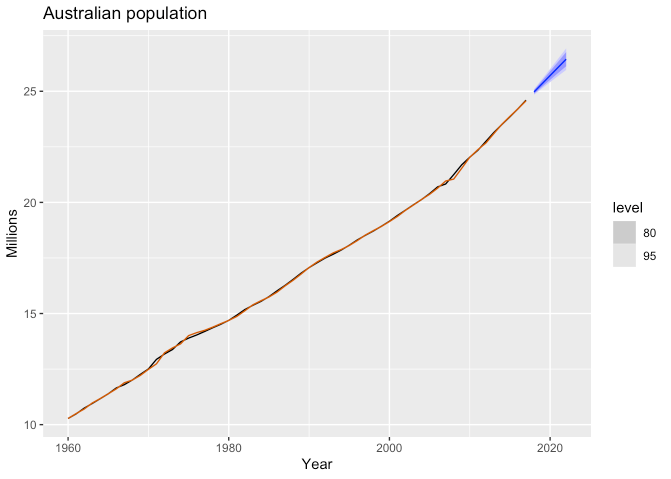
Damped trend methods
- 위의 Holt’s linear trend method에 의해 예측되는 값은 조금 더 긴 예측 기간에 대해서 과도하게 예측하는 경향이 있다고 합니다.
- 이러한 부분을 어느 정도 보안하는 방법으로 미래의 어느 시점에서 추세를 평평하게 완화하는 매개변수를 도입한 방법이 있습니다.
- Gradner & McKenize (1985)는 아래와 같이 0과 1 사이 값인 감쇠 매개변수(dampens parameter)를 도입하였습니다.
\[\hat{y}_{t+h|t} = l_{t} + (\phi + \phi^2 + ... + \phi^{h})b_{t}\] \[l_{t} = \alpha y_{t} + (1-\alpha)(l_{t-1} + \phi b_{t-1})\] \[b_{t} = \beta^{*}(l_{t}-l_{t-1}) + (1-\beta^{*})\phi b_{t-1}\]
- 여기서 \(\phi = 1\)이면 이 방법은 holt’s의 방법과 동일합니다.
- 이 감쇠 매개변수로 인해 단기 예측은 일정한 추세는 살리지만 장기로 갈수록 일정하게 만듭니다.
- 일반적으로 이 감쇠 매개변수는 최소 0.8에서 최대 0.98까지 둔다고 합니다.
- 아래 예시 코드로 비교해보겠습니다.
- 감쇠 방법에는 trend term에 “Ad”가 들어갑니다.
aus_economy %>%
model(
`Holt's method` = ETS(Pop ~ error("A") + trend("A") + season("N")),
`Damped Holt's method` = ETS(Pop ~ error("A") + trend("Ad", phi = 0.9) + season("N"))
) %>%
forecast(h = 15) %>%
autoplot(aus_economy, level = NULL) +
labs(y = "Millions", title = "Australian population") +
guides(color = guide_legend(title = "Forecast method"))
- 또 다른 예시입니다. 100분 동안 관찰된 1분 당 인터넷 사용자 수 데이터입니다.
www_usage <- WWWusage %>%
as_tsibble()
www_usage## # A tsibble: 100 x 2 [1]
## index value
## <dbl> <dbl>
## 1 1 88
## 2 2 84
## 3 3 85
## 4 4 85
## 5 5 84
## 6 6 85
## 7 7 83
## 8 8 85
## 9 9 88
## 10 10 89
## # … with 90 more rowswww_usage %>%
autoplot(value) +
labs(x = "Minute", y = "Number of users", title = "Internet usage per minute")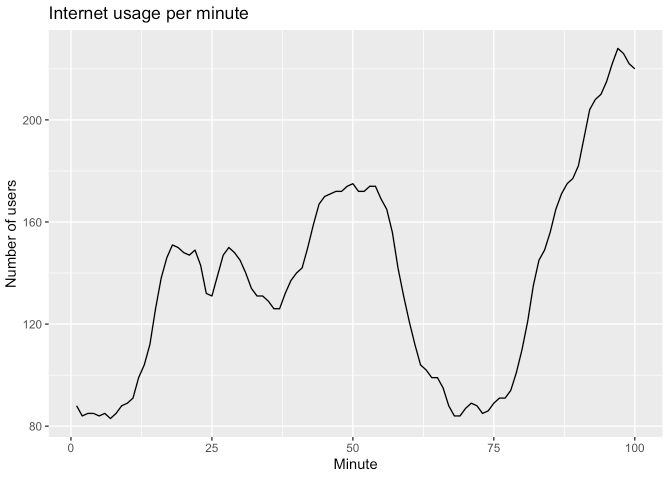
- 시계열 교차검증을 사용하여 아래 세 가지 방법의 1단계 예측 정확도를 비교해봅니다.
stretch_tsibble()함수는 관측치들을 여러 조각들로 롤링(rolling) 해주는 역할을 합니다.
www_usage %>%
stretch_tsibble(.init = 10) %>%
model(
`SES` = ETS(value ~ error("A") + trend("N") + season("N")),
`Holt` = ETS(value ~ error("A") + trend("A") + season("N")),
`Damped` = ETS(value ~ error("A") + trend("Ad") + season("N"))
) %>%
forecast(h = 1) %>%
accuracy(www_usage)## Warning: The future dataset is incomplete, incomplete out-of-sample data will be treated as missing.
## 1 observation is missing at 101## # A tibble: 3 x 10
## .model .type ME RMSE MAE MPE MAPE MASE RMSSE ACF1
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 Damped Test 0.288 3.69 3.00 0.347 2.26 0.663 0.636 0.336
## 2 Holt Test 0.0610 3.87 3.17 0.244 2.38 0.701 0.668 0.296
## 3 SES Test 1.46 6.05 4.81 0.904 3.55 1.06 1.04 0.803- RMSE 값으로 비교해본 결과 Damped Holt’s method가 가장 좋습니다.
- 따라서 감쇠 방법으로 예측 추이를 확인해보겠습니다.
fit <- www_usage %>%
model(`Damped` = ETS(value ~ error("A") + trend("Ad") + season("N")))
fit %>%
report()## Series: value
## Model: ETS(A,Ad,N)
## Smoothing parameters:
## alpha = 0.9999
## beta = 0.9966439
## phi = 0.814958
##
## Initial states:
## l[0] b[0]
## 90.35177 -0.01728234
##
## sigma^2: 12.2244
##
## AIC AICc BIC
## 717.7310 718.6342 733.3620fit %>%
tidy()## # A tibble: 5 x 3
## .model term estimate
## <chr> <chr> <dbl>
## 1 Damped alpha 1.00
## 2 Damped beta 0.997
## 3 Damped phi 0.815
## 4 Damped l[0] 90.4
## 5 Damped b[0] -0.0173- 기울기에 대한 평활화 매개변수 \(\beta\)는 거의 1에 가깝게 추정되며, \(\alpha\) 또한 1에 가까운 수준으로 새로운 관측치에 대해 강력하게 반응하는 것으로 보여집니다.
fit %>%
forecast(h = 10) %>%
autoplot(www_usage) +
labs(x = "Minute", y = "Number of users", title = "Internet usage per minute")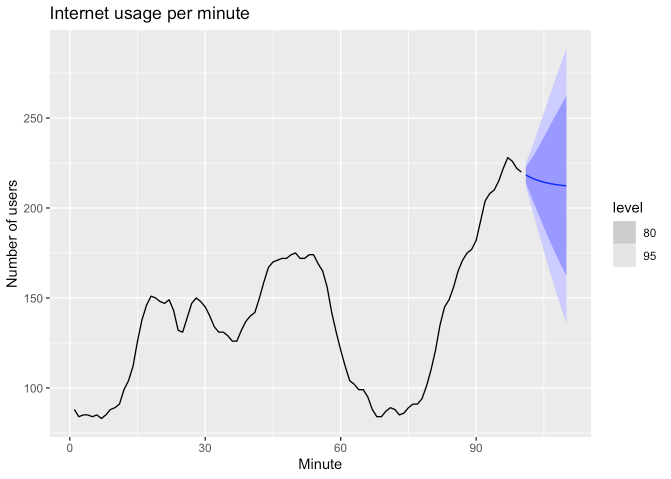
Methods with seasonality
- 추세성 뿐만 아니라 계절성까지 확보하기 위해 위의 Holt 방법을 확장했습니다. (Holt & Winters, 1960)
- 여기에는 위의 매개변수 \(\alpha\), \(\beta^{*}\)에 추가로 계절성에 대한 smoothing parameter \(\gamma\)까지 고려가 됩니다.
- 이 방법에는 계절 성분의 특성에 따라 두 가지로 나누어서 적용해볼 수 있습니다.
- 계절적 변동이 전반적으로 거의 일정한 편일 때는 가산법(additive)이 선호되고
비례하여 변동이 있을 때는 승법(multiplicative)이 선호됩니다.
- 계절적 변동이 전반적으로 거의 일정한 편일 때는 가산법(additive)이 선호되고
- 수식에 대한 접근은 아래 링크를 통해서 확인 부탁드립니다!
- 바로 예시로 접근하겠습니다. 마찬가지로
tsibbledata라이브러리 내tourism데이터를 활용합니다.- 분기별 호주 관광객 수를 나타낸 데이터로, 예시에서는 휴가철에 방문객 수 예측을 목적으로 합니다.
aus_holidays <- tourism %>%
filter(Purpose == "Holiday") %>%
summarise(Trips = sum(Trips/1000))
aus_holidays## # A tsibble: 80 x 2 [1Q]
## Quarter Trips
## <qtr> <dbl>
## 1 1998 Q1 11.8
## 2 1998 Q2 9.28
## 3 1998 Q3 8.64
## 4 1998 Q4 9.30
## 5 1999 Q1 11.2
## 6 1999 Q2 9.61
## 7 1999 Q3 8.91
## 8 1999 Q4 9.03
## 9 2000 Q1 11.1
## 10 2000 Q2 9.20
## # … with 70 more rowsfit <- aus_holidays %>%
model(
`additive` = ETS(Trips ~ error("A") + trend("A") + season("A")),
`multiplicative` = ETS(Trips ~ error("M") + trend("A") + season("M"))
)
fc <- fit %>%
forecast(h = "3 years")
fc %>%
autoplot(aus_holidays, level = NULL) +
labs(y = "Overnight trips (millions)", title = "Australian domestic tourism") +
guides(color = guide_legend(title = "Forecast"))
- 아래
glance()함수를 사용하여 모형 평가 메트릭을 확인해본 결과 MSE가 더 낮은 것은 승법모형으로 보여집니다.
fit %>%
glance()## # A tibble: 2 x 9
## .model sigma2 log_lik AIC AICc BIC MSE AMSE MAE
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 additive 0.193 -105. 229. 231. 250. 0.174 0.184 0.321
## 2 multiplicative 0.00212 -104. 227. 229. 248. 0.170 0.183 0.0328
Holt-Winters’ damped method
- 마찬가지로 이 방법 또한 감쇠법이 가능합니다. 바로 예시로 살펴보겠습니다.
sth_cross_ped <- pedestrian %>%
filter(Date >= "2016-07-01", Sensor == "Southern Cross Station") %>%
index_by(Date) %>%
summarise(Count = sum(Count)/1000)
sth_cross_ped## # A tsibble: 184 x 2 [1D]
## Date Count
## <date> <dbl>
## 1 2016-07-01 17.6
## 2 2016-07-02 2.52
## 3 2016-07-03 1.73
## 4 2016-07-04 17.3
## 5 2016-07-05 16.5
## 6 2016-07-06 16.8
## 7 2016-07-07 17.0
## 8 2016-07-08 17.2
## 9 2016-07-09 3.21
## 10 2016-07-10 1.75
## # … with 174 more rowssth_cross_ped %>%
filter(Date <= "2016-07-31") %>%
model(hw = ETS(Count ~ error("M") + trend("Ad") + season("M"))) %>%
forecast(h = "2 weeks") %>%
autoplot(sth_cross_ped %>% filter(Date <= "2016-08-14")) +
labs(y = "Pedestrians ('000)", title = "Daily traffic: Southern Cross")
- 모형은 데이터의 끝부분에서 주간 계절성 패턴과 증가 추세를 충분히 식별했다는 점을 확인할 수 있습니다.
Model selection
- ETS 통계 프레임워크의 가장 큰 장점은 정보 기준을 모형 선택에 사용할 수 있다는 점입니다.
- AIC, AICs 및 BIC 등이 있습니다.
- \(k\)는 모형에서 주어진 매개변수의 갯수이고 \(L\)은 모형의 우도값(likelihood)라고 할 때 아래와 같이 표현할 수 있습니다.
\[\text{AIC} = -2\log{L} + 2k\] \[\text{AIC}_{c} = AIC + \frac{2k(k+1)}{T-k-1}\] \[BIC = AIC + k(\log{T}-2)\]
- 아래 예시를 통해 살펴보겠습니다.
- 기존 위에서 보였던 예시들은
ETS()함수내에formula항을 모두 직접 정의하였지만 단순히 종속변수만 인자로 받을 경우ETS()함수는 \(\text{AIC}_{c}\)를 최소로하는 모델을 선택해줍니다.
fit <- aus_holidays %>%
model(ETS(Trips))
fit %>%
report()## Series: Trips
## Model: ETS(M,N,A)
## Smoothing parameters:
## alpha = 0.3484054
## gamma = 0.0001000018
##
## Initial states:
## l[0] s[0] s[-1] s[-2] s[-3]
## 9.727072 -0.5376106 -0.6884343 -0.2933663 1.519411
##
## sigma^2: 0.0022
##
## AIC AICc BIC
## 226.2289 227.7845 242.9031components()함수를 사용하여 각 모형의 성분들 값을 확인할 수 있습니다.
fit %>%
components() %>%
autoplot() +
labs(title = "ETS(M, N, A) components")## Warning: Removed 4 row(s) containing missing values (geom_path).
fit %>%
augment() %>%
autoplot(.resid)
fit %>%
augment() %>%
autoplot(.innov)
'time-series (tidy approach)' 카테고리의 다른 글
| [R] 7. ARIMA (AutoRegressive Integrated Moving Average) (0) | 2021.08.06 |
|---|---|
| [R] 5. Time-series Regression (0) | 2021.07.29 |
| [R] 4. feasts (0) | 2021.07.28 |
| [R] 3. tsibbledata (0) | 2021.07.28 |
| [R] 2. tsibble (0) | 2021.07.27 |

