[R] 7. ARIMA (AutoRegressive Integrated Moving Average)
library(fpp3)
#library(fable)Stationarity and differencing
- 정상성(Stationarity)과 차분(differencing)
- 정상 시계열이란?
- 통계적 특징들이 관측되는 시점에 의존되지 않는 시계열을 말합니다.
- 따라서 추세가 있는 시계열 또는 계절성이 있는 시계열들을 정상성이 있다고 보기 어려우며, 추세와 계절성은 다른 시점의 시계열 값에 영향을 줍니다.
- 차분이란?
- 연속적으로 측정된 관측치 간의 차이를 계산하는 것을 차분이라고 하며, 비정상 시계열을 정상으로 만들어 주는 방법 중 하나 입니다.
- 차분은 시계열의 추세와 계절성을 제거 또는 축소하여 시계열의 평균을 안정화하는데 도움이 될 수 있습니다.
- 관측치 간의 차이 간격 n에 따라 n차 차분이 있을수도 있으며, 때에 따라 2차 차분까지도 진행될 수 있습니다.
- 그 외 로그 변환도 시계열의 분산을 안정화하는데 도움이 될 수 있습니다.
- 또한 ACF 그래프는 비정상 시계열을 식별하는데 도움이 됩니다.
- 정상 시계열의 경우 ACF는 상대적으로 빠르게 0으로 떨어지는 반면 비정상 시계열은 천천히 감소합니다.
- 또한 비정상 시계열의 경우 값이 더 크고 양수인 경우가 많습니다.
Random walk model
\[y_{t} - y_{t-1} = \epsilon_{t}\] - \(\epsilon_{t}\)를 white noise 라고 정의할 때 아래 정의를 랜덤 워크 모형이라고 부릅니다.
\[y_{t} = y_{t-1} + \epsilon_{t}\]
- 랜덤 워크 모형은 비정상 시계열의 대표적인 예이며 재무 및 경제 분야에서도 널리 사용됩니다.
- 이 모형의 예측은 마지막 관측치와 동일합니다.
- 미래의 움직임은 예측할 수 없고, 오르거나 내리거나 할 가능성도 동일하기 떄문
Seasonal differencing
- 차분도 특정 시점 전의 관측치를 뺴는 것처럼 계절 단위로도 차분이 가능합니다.
- 시계열 데이터가 정상성을 얻기 위해서는 1차 차분과 계절 차분 모두 취해야하는 경우가 있습니다.
- 아래 예시로 확인하시길 바랍니다.
PBS %>%
filter(ATC2 == "H02") %>%
summarise(Cost = sum(Cost)/1000000) %>%
transmute(
`Sales ($million)` = Cost,
`Log sales` = log(Cost),
`Annual change in log sales` = difference(log(Cost), 12), # Annual data이기에 12
`Doubly differenced log sales` = difference(difference(log(Cost), 12), 1)
) %>%
pivot_longer(
cols = -Month,
names_to = "Type",
values_to = "Sales"
) %>%
mutate(Type = factor(Type, levels = c("Sales ($million)",
"Log sales",
"Annual change in log sales",
"Doubly differenced log sales"))) %>%
ggplot(aes(x = Month, y = Sales)) +
geom_line(size = 0.7) +
facet_wrap(. ~ Type, scales = "free_y", nrow = 4) +
labs(title = "Coricosteroid durg sales", y = NULL)
- 계절 차분을 먼저 한 이후 1차 차분을 진행하는 것이 좋습니다.
- 1차 차분 먼저 수행하게되면 여전히 계절성이 존재할 가능성이 있기 때문입니다.
Unit root tests
- 차분이 필요한지 아닌지를 판단할 수 있는 객관적인 방법 중 하나로 단위 루트 검정을 사용하는 것 입니다.
- 이는 정상성에 대한 통계적 가설 검정 기법 중 하나입니다.
- 여기에서는 KPSS(Kwiatkowski-Phillips-Schmidt-Shin) 테스트를 사용합니다.
- 이 검정에서 귀무 가설은 “데이터가 정상성을 만족한다” 입니다.
- 결과적으로 p-value가 유의수준 이하이면 귀무가설을 기각하므로 차분이 필요함을 나타냅니다.
- 이 검정법은
features()함수를 같이 사용하여unitroot_kpss()함수로 진행할 수 있습니다.
aus_total_retail <- aus_retail %>%
summarise(Turnover = sum(Turnover))
aus_total_retail %>%
mutate(log_turnover = log(Turnover)) %>%
features(.var = log_turnover, feature = unitroot_kpss)## # A tibble: 1 x 2
## kpss_stat kpss_pvalue
## <dbl> <dbl>
## 1 7.35 0.01- 통계량의 유의수준이 0.05보다 작으므로 귀무가설을 기각합니다. 즉, 차분을 할 필요가 있다는 뜻입니다.
- 그렇다면 몇차 차분이 필요할까요?
- 그에 대한 답변은
unitroot_nsdiffs()또는unitroot_ndiffs()함수를 통해 구할 수 있습니다.unitroot_nsdiffs()는 계절 차분에 대해서unitroot_ndiffs()는 일반 n차 차분에 대해서
aus_total_retail %>%
mutate(log_turnover = log(Turnover)) %>%
features(.var = log_turnover, feature = unitroot_nsdiffs)## # A tibble: 1 x 1
## nsdiffs
## <int>
## 1 1aus_total_retail %>%
mutate(log_turnover = difference(log(Turnover), 12)) %>%
features(.var = log_turnover, feature = unitroot_ndiffs)## # A tibble: 1 x 1
## ndiffs
## <int>
## 1 1aus_total_retail %>%
mutate(log_turnover = difference(difference(log(Turnover), 12), 1)) %>%
features(.var = log_turnover, feature = unitroot_ndiffs)## # A tibble: 1 x 1
## ndiffs
## <int>
## 1 0- 즉, 위 결과를 통해 해당 시계열 데이터는 1차 계절차분과 1차 차분이 필요했음을 확인할 수 있었습니다.
Autoregressive models
- 이전에 다중 회귀 모형에서는 변수들의 선형 조합( linear combination)을 이용하여 예측했습니다.
- 자기 회귀 모형에서는 변수들의 과거 값들의 선형 조합을 이용하여 예측합니다.
- 자기회귀(autoregressive)라는 단어에는 자기 자신에 대한 변수의 회귀라는 의미가 있습니다.
- 차수 \(p\)에 대한 자기회귀 모형은 아래와 같이 정의할 수 있습니다.
\[y_{t} = c + \phi_{1}y_{t-1} + \phi_{2}y_{t-2} + ... + \phi_{p}y_{t-p} + \epsilon_{t}\]
- 이를 \(p\)차 자기회귀 모형인 \(\text{AR}(p)\) 모형이라고 부릅니다.
- 모형에 따른 제한 조건들이 필요한데 상세한 부분은 여기 페이지 하단 부분을 참고하시면 됩니다!
Moving average models
- 이동 평균 모형에서는 다중 회귀 모형과 비슷해보이나 과거의 예측 오차(forecast error)를 활용합니다.
\[y_{t} = c + \epsilon_{t} + \theta_{1}\epsilon_{t-1} + \theta_{2}\epsilon_{t-2} + ... + \theta_{q}\epsilon_{t-q}\]
- 이를 \(q\)차 이동 평균 모형인 \(\text{MA}(q)\) 모형이라고 부릅니다.
- \(y_t{t}\)의 값을 과거 몇 개의 예측 오차의 가중 이동 평균으로 고려해볼 수 있다는 점에 주목하시면 됩니다.
- 이동 평균 평활(smoothing)과 헷갈리시면 안됩니다.
- 이동 평균 모형은 미래 값을 예측할 때 사용하지만 평활은 과거 추세-주기를 측정할 떄 사용합니다.
- 마찬가지로 모형에 필요한 제한 사항들은 여기 페이지 하단 부분을 읽어주세요!
Non-seasonal ARIMA models
- 차분하는 과정과 자귀회귀(AR), 그리고 이동평균(MA) 모형을 결합하면 비계절성 ARIMA 모형을 얻을 수 있습니다.
- ARIMA는 AutoRegressive Integrated Moving Average (이동 평균을 누적한 자기 회귀)의 약자입니다.
- 모형 식은 아래와 같습니다.
\[y_{t}^{'} = c + \phi_{1}+y_{t-1}^{'} + ... + \phi_{p}+y_{t-[]}^{'} + \theta_{1}\epsilon_{t-1} + ... + \theta_{q}\epsilon_{t-q} + \epsilon_{t}\]
- 위 식에서 좌변 \(y_{t}^{'}\)는 차분을 통해 얻은 시계열 입니다.
- 우변은 시차 값과 시차 오차(lagged error) 둘 다를 포함합니다.
- 이를 \(\text{ARIMA}(p, d, q)\) 모형이라고 부릅니다.
- \(d\)는 몇차 차분이 들어갔는 지를 의미 합니다.
- 이제부터 예시를 통해 살펴보겠습니다.
- 아래 그래프는 1960년부터 2017년까지 이집트 국가의 GDP 대비 수출의 비율을 보여줍니다.
global_economy %>%
filter(Code == "EGY") %>%
autoplot(Exports) +
labs(y = "% of GDP", title = "Egyptian Exports")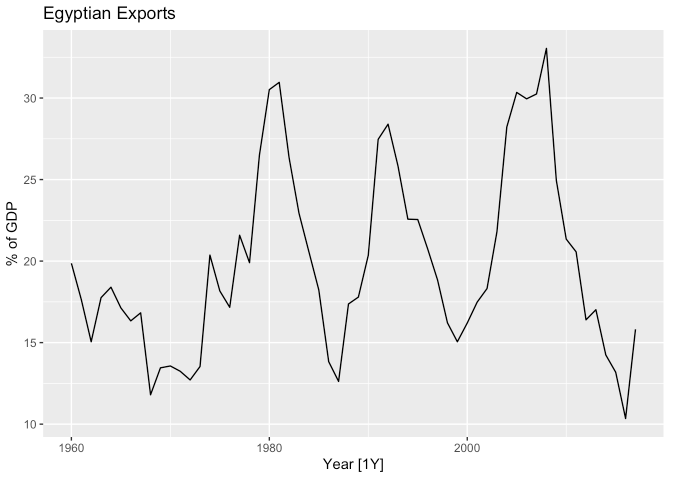
- ARIMA 모형을 적용하는 함수는
ARIMA()입니다. ARIMA 모형의 각 차수 값을 자동으로 선택해줍니다.
fit <- global_economy %>%
filter(Code == "EGY") %>%
model(ARIMA(Exports))fit %>%
report()## Series: Exports
## Model: ARIMA(2,0,1) w/ mean
##
## Coefficients:
## ar1 ar2 ma1 constant
## 1.6764 -0.8034 -0.6896 2.5623
## s.e. 0.1111 0.0928 0.1492 0.1161
##
## sigma^2 estimated as 8.046: log likelihood=-141.57
## AIC=293.13 AICc=294.29 BIC=303.43- 위 결과와 같이 \(\text{ARIMA}(2, 0, 1)\) 모형이 적합되었습니다.
- 이를 기반으로 하는 예측은 아래와 같습니다.
fit %>%
forecast(h = 10) %>%
autoplot(global_economy) +
labs(y = "% of GDP", title = "Egyptian Exports")
Understanding ARIMA models
- 모든 차수들을 코드에 의해 자동으로 결정하게 두면 편리하긴 하지만 그래도 모델이 대략적으로 작동하는 방식은 익혀둘 필요가 있습니다.
- 모형에서 상수 값 \(c\)는 장기 예측값에 중요한 영향을 줍니다.
- \(c=0\)이고 \(d=0\)이면, 장기 예측값이 0에 가까워질 가능성이 높습니다.
- \(c=0\)이고 \(d=1\)이면, 장기 예측값이 0이 아닌 상수에 가까워질 가능성이 높습니다.
- \(c=0\)이고 \(d=2\)이면, 장기 예측값이 직선 형태로 나타날 가능성이 높습니다.
- \(c\neq0\)이고 \(d=0\)이면, 장기 예측값이 데이터의 평균에 가까워질 가능성이 높습니다.
- \(c\neq0\)이고 \(d=1\)이면, 장기 예측값이 직선 형태로 나타날 가까워질 가능성이 높습니다.
- \(c\neq0\)이고 \(d=2\)이면, 장기 예측값이 2차 곡선 추세로 나타날 가능성이 높습니다.
- \(d\) 값은 예측 구간(prediction interval)에도 영향을 줍니다.
- \(d\) 값이 클수록 예측 구간의 크기가 더욱 급격하게 늘어납니다.
ACF and PACF plots
- 보통 단순하게 시계열 그래프만 보고나서 \(p\), \(q\) 값이 데이터에 맞았는지 이야기하기 어렵습니다.
- 따라서 ACF, PACF 그래프를 참고할 필요도 있습니다.
- \(y_{t}\)와 \(y_{t-k}\)의 관계를 측정하는 자기상관 ACF 그래프를 생각해본다면..
\(y_{t}\)와 \(y_{t-1}\)이 상관관계가 있다면, \(y_{t-1}\), \(y_{t-2}\)에도 상관관계가 있어야 합니다. - 하지만 \(y_{t}\)와 \(y_{t-2}\)는 값에 종속보다 두 값 모두 \(y_{t-1}\)과 관련이 있어서 상관관계를 가질 수도 있습니다.
- 이러한 문제를 극복하기 위해 부분 자기상관(partial autocorrelations)을 이용할 수 있습니다.
- 이 값은 시차의 효과를 제거한 후 \(y_{t}\)와 \(y_{t-k}\) 사이의 관계를 측정합니다.
- 이 두 개의 값을 구하는 함수는
ACF()와PACF()입니다.
global_economy %>%
filter(Code == "EGY") %>%
ACF(Exports) %>%
autoplot()
global_economy %>%
filter(Code == "EGY") %>%
PACF(Exports) %>%
autoplot()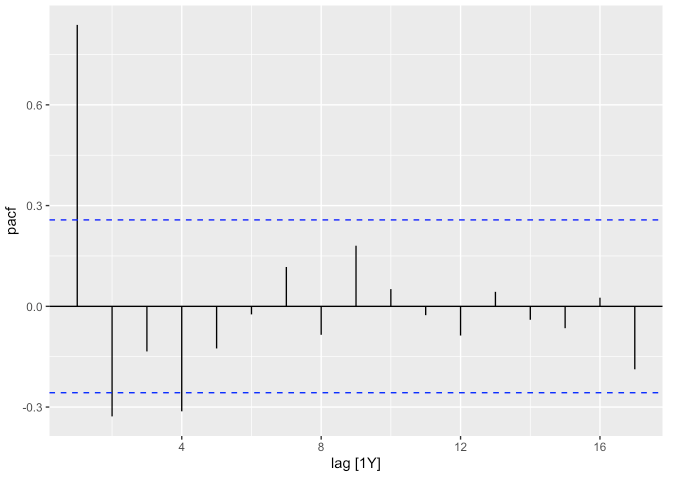
- 한 번에 ACF, PACF 두 개의 그래프를 그리고 싶다면 아래 코드처럼
gg_tsdisplay()함수를 이용하시면 됩니다.
global_economy %>%
filter(Code == "EGY") %>%
gg_tsdisplay(Exports, plot_type = "partial")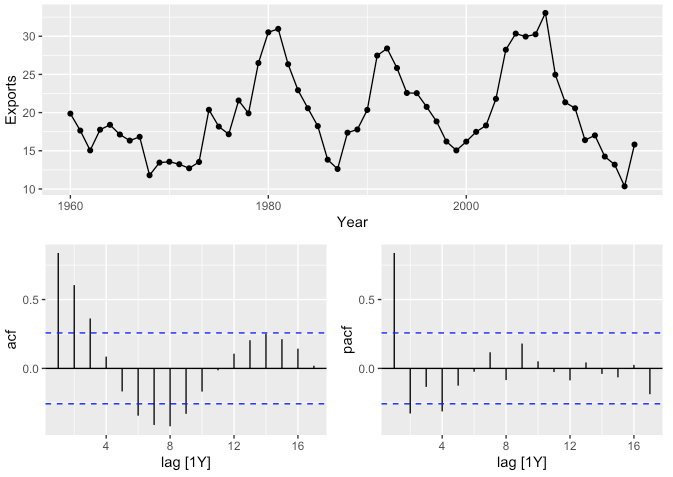
- 이러한 그래프 해석은 다음과 같이 해볼 수 있습니다.
- 아래와 같이 나타날 경우 데이터는 \(\text{ARIMA}(p, d, 0)\) 모형을 따를 수도 있습니다.
- ACF가 지수적으로 감소하거나 \(\sin(x)\) 모양인 경우
- 또는 PACF에서 시차 \(p\)에 뾰족한 막대가 유의미하게 있지만 시차 \(p\) 이후에는 없을 때
- 아래와 같이 나타날 경우 데이터는 \(\text{ARIMA}(0, d, q)\) 모형을 따를 수도 있습니다.
- PACF가 지수적으로 감소하거나 \(\sin(x)\) 모양인 경우
- 또는 ACF에서 시차 \(q\)에 뾰족한 막대가 유의미하게 있지만 시차 \(q\) 이후에는 없을 때
- 아래와 같이 나타날 경우 데이터는 \(\text{ARIMA}(p, d, 0)\) 모형을 따를 수도 있습니다.
- 이런 관점에서 다시 위의 ACF, PACF 그래프를 본다면..
- ACF는 \(\sin(x)\) 함수 형태와 유사한 편이고
- PACF는 4번째 시차에서 마지막으로 유의미한 뾰족 막대를 보입니다.
- 따라서 이 데이터는 \(\text{ARIMA}(4, 0, 0)\) 모형을 기대해볼 수도 있습니다.
ARIMA()에서 자동이 아닌 수동으로 차수를 지정하여 모형을 적합시킬 때에는pdq()를 활용합니다.
fit2 <- global_economy %>%
filter(Code == "EGY") %>%
model(ARIMA(Exports ~ pdq(4, 0, 0)))
fit2 %>%
report()## Series: Exports
## Model: ARIMA(4,0,0) w/ mean
##
## Coefficients:
## ar1 ar2 ar3 ar4 constant
## 0.9861 -0.1715 0.1807 -0.3283 6.6922
## s.e. 0.1247 0.1865 0.1865 0.1273 0.3562
##
## sigma^2 estimated as 7.885: log likelihood=-140.53
## AIC=293.05 AICc=294.7 BIC=305.41- 그 결과 AICc 값은 \(\text{ARIMA}(2, 0, 1)\) 모형이 조금 더 낮으므로 더 나은 모형이라고 생각할 수 있습니다.
Estimation and order selection
Maximum likelihood estimation
- 모형의 차수(\(p\), \(d\), \(q\))를 찾은 다음 상수항 \(c\)와 \(\theta\), \(\phi\) 매개 변수를 추정해야 합니다.
- R에서는 ARIMA 모형을 계산할 때 MLE(Maximum Likelihood Estimation)를 사용합니다.
- 아래와 같이 오차항을 최소화하는 최소제곱 추정과 비슷합니다.
\[\sum_{t=1}^{T} \epsilon_{t}^{2}\] - 해당 라이브러리에서 쓰인 ARIMA() 함수는 매개변수 값을 추정할 때 로그가능도함수를 최대화하는 값을 기반으로 찾습니다.
Information Criteria
- 아카이케 정보 기준(AIC)은 ARIMA 모델에서 차수를 결정할 때도 유용합니다.
- \(L\)은 바로 위에서 언급한 가능도함수
- \(c\neq0\)이면 \(k=1\), \(c=0\)이면 \(k=0\)
\[\text{AIC} = -2\log(L) + 2(p+q+k+1)\]
- ARIMA에서 수정된 AIC(AICc)는 아래와 같습니다.
\[\text{AIC}_{c}=\text{AIC}+\frac{2(p+q+k+1)(p+q+k+2)}{T-p-q-k-2}\]
- 참고로 AICc를 활용한 모형 선택은 같은 차수로 차분을 한 ARIMA 모형에서만 의미가 있습니다.
ARIMA modelling in fable
How does ARIMA() work?
fable라이브러리에서ARIMA()함수는 AICc 및 MLE를 최소화를 결합한 Hyndman-Khandakar 알고리즘을 사용한다고 합니다.- 자동화된 ARIMA 모델링을 위한 힌드만-칸다카르 알고리즘을 정말 아주 간략하게만 요약해보면 아래 과정입니다.
-
- KPSS 검정을 반복하여 차분 횟수를 결정합니다. (\(0 \le d \le 2\))
- 데이터를 \(d\)번 차분한 후 AICc를 최소화하여 \(p\)와 \(q\)를 결정합니다. (stepwise exploration)
-
Modelling procedure
- 일반적으로 ARIMA 모형에 시계열 데이터 세트를 적합할 때 아래와 같은 절차를 가집니다.
-
- 데이터를 시각화해보고 이상치들을 식별합니다.
- 필요한 경우 데이터를 변환하여 분산을 안정화합니다. (Box-Cox 변환 사용)
- 데이터가 정상성을 나타내지 않는다면, 데이터가 정상성을 나타날 때까지 데이터를 가지고 1차 차분을 계산합니다.
- ACF, PACF를 살펴봅니다. \(\text{ARIMA}(p, d, 0)\) 또는 \(\text{ARIMA}(0, d, q)\) 어느 것이 적절한지..
- 그외 다른 모형도 적합해보고 더 나은 모형을 찾기 위해 AICc를 활용하여 점검합니다.
- 잔차의 ACF를 그려보고 검정하여 확인합니다. 잔차가 특별한 패턴을 보이지 않는다면 (백색잡음) 예측 값을 계산합니다.
-
- 본격 예시입니다. 비슷하게
global_economy데이터를 활용하여 중앙아프리카의 수출량을 확인해보겠습니다.
global_economy %>%
filter(Code == "CAF") %>%
autoplot(Exports) +
labs(y = "% of GDP", title = "Central African Republic exports")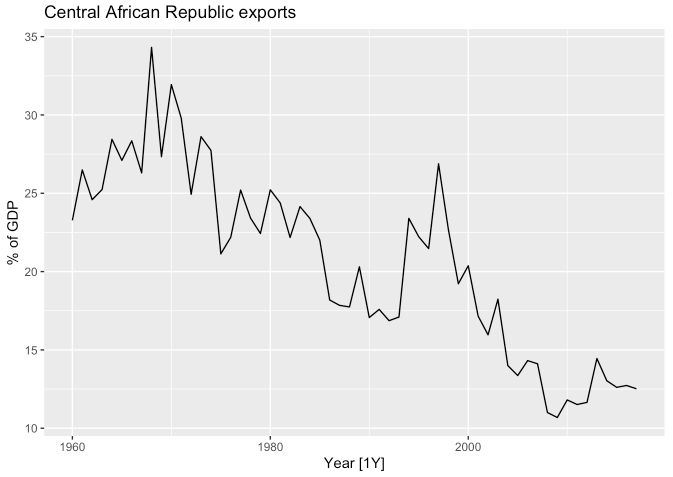
- 위 그래프는 감소 추세와 더불어 일부 비정상성을 보입니다.
- 또한 분산의 변화 증거가 없으므로 Box-Cox 변환은 스킵합니다.
- 비정상성을 해결하기 위해
gg_tsdisplay()함수를 적용하여 1차 차분을 적용한 후 ACF, PACF 그래프를 확인해봅니다.
global_economy %>%
filter(Code == "CAF") %>%
gg_tsdisplay(difference(Exports, 1), plot_type = "partial")## Warning: Removed 1 row(s) containing missing values (geom_path).## Warning: Removed 1 rows containing missing values (geom_point).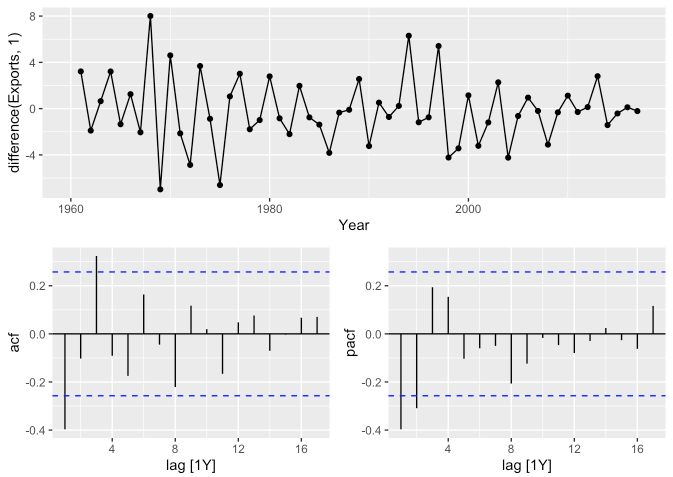
- 어느 정도 비정상성이 해소된 것처럼 보입니다.
ACF 그래프를 보면 \(q=3\)인 ARIMA(0, 1, 3), PACF 그래프를 보면 \(p=2\)인 ARIMA(2, 1, 0)가 적당할 것 같습니다. - 따라서 두 개의 모형과 더불어 또 다른 하나는 차수를 자동 선택하게끔(stepwise), 또 다른 하나는 전반적인 탐색을 위한 모형(search)을 적합시킵니다.
caf_fit <- global_economy %>%
filter(Code == "CAF") %>%
model(
arima013 = ARIMA(Exports ~ pdq(0, 1, 3)),
arima210 = ARIMA(Exports ~ pdq(2, 1, 0)),
stepwise = ARIMA(Exports),
search = ARIMA(Exports, stepwise = FALSE)
)
caf_fit %>%
pivot_longer(
cols = 2:5,
names_to = "ModelName",
values_to = "Orders"
)## # A mable: 4 x 3
## # Key: Country, ModelName [4]
## Country ModelName Orders
## <fct> <chr> <model>
## 1 Central African Republic arima013 <ARIMA(0,1,3)>
## 2 Central African Republic arima210 <ARIMA(2,1,0)>
## 3 Central African Republic stepwise <ARIMA(2,1,2)>
## 4 Central African Republic search <ARIMA(3,1,0)>caf_fit %>%
select(stepwise) %>%
report()## Series: Exports
## Model: ARIMA(2,1,2)
##
## Coefficients:
## ar1 ar2 ma1 ma2
## -0.6741 -0.7142 0.2468 0.4831
## s.e. 0.1821 0.2037 0.2531 0.2576
##
## sigma^2 estimated as 6.416: log likelihood=-132.1
## AIC=274.2 AICc=275.37 BIC=284.41caf_fit %>%
select(search) %>%
report()## Series: Exports
## Model: ARIMA(3,1,0)
##
## Coefficients:
## ar1 ar2 ar3
## -0.4419 -0.1850 0.2055
## s.e. 0.1295 0.1385 0.1274
##
## sigma^2 estimated as 6.519: log likelihood=-133
## AIC=274 AICc=274.77 BIC=282.18caf_fit %>%
glance() %>%
arrange(AICc) %>%
select(.model, AICc)## # A tibble: 4 x 2
## .model AICc
## <chr> <dbl>
## 1 search 275.
## 2 arima210 275.
## 3 arima013 275.
## 4 stepwise 275.- 네 가지 모형은 거의 동일한 AICc 값을 같습니다.
그나마 근소하게 search 이름으로 적합된 ARIMA(3, 1, 0)이 가장 낮은 AICc 값을 보입니다. - 따라서 해당 모형을 가지고
gg_tsresiduals()함수를 사용하여 잔차의 백색잡음 여부와 잔차의 ACF를 확인해봅니다.
caf_fit %>%
select(search) %>%
gg_tsresiduals()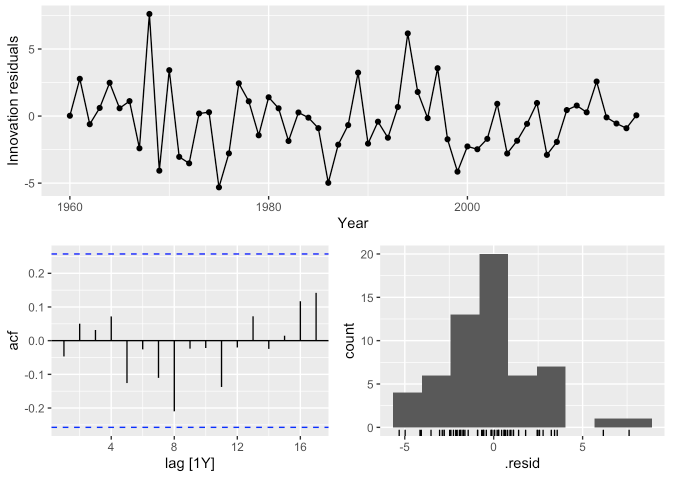
ljung_box를 적용하여 포트멘토 검정(portmanteau)도 해볼 수 있습니다.lag는 계산에 쓰일 시차 자기상관 계수의 수dof는 적합된 모형의 자유도
caf_fit %>%
augment() %>%
filter(.model == "search") %>%
features(
.var = .innov,
features = ljung_box,
lag = 10,
dof = 3
)## # A tibble: 1 x 4
## Country .model lb_stat lb_pvalue
## <fct> <chr> <dbl> <dbl>
## 1 Central African Republic search 5.75 0.569- p-value가 유의수준 보다 크게 나왔습니다. 해당 잔차는 백색잡음(유의미한 패턴이 없음)임을 확인할 수 있습니다.
- 마지막으로
forecast()함수를 사용하여 예측값을 확인할 수 있습니다.
caf_fit %>%
select(Country, search) %>%
forecast(h = 5) %>%
autoplot(global_economy)
'time-series (tidy approach)' 카테고리의 다른 글
| [R] 6. Exponential smoothing (0) | 2021.07.29 |
|---|---|
| [R] 5. Time-series Regression (0) | 2021.07.29 |
| [R] 4. feasts (0) | 2021.07.28 |
| [R] 3. tsibbledata (0) | 2021.07.28 |
| [R] 2. tsibble (0) | 2021.07.27 |

